Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
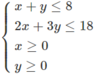
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
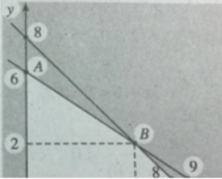
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.

a)
Để quy hoạch x sào đất trồng cà tím, cần \(200\,000.x\)(đồng)
Để quy hoạch y sào đất trồng cà chua, cần \(100\,000.y\)(đồng)
Tổng số tiền để mua hạt giống là \(200{\rm{ }}000.x + 100{\rm{ }}000.y\) (đồng), tối đa là 9 triệu đồng nên ta có bất phương trình: \(0,2x + 0,1y \le 9\)
Ngoài ra số sào đất là số không âm nên \(x \ge 0\) và \(y \ge 0\)
b) + Cặp số (20; 40) thỏa mãn cả 3 bất phương trình trên vì \(0,2.20 + 0,1.40 = 8 < 9\).
+ Cặp số (40; 20) không thỏa mãn các bất phương trình trên vì \(0,2.40 + 0,1.20 = 10 > 9\).
+ Cặp số (-30; 10) không thỏa mãn các bất phương trình trên vì \( - 30 < 0\).

a) Gọi chiều dài mảnh vườn là a(m)
Khi đó ta có \(2a + 2x = 40 \Leftrightarrow a = 20 - x\)
Vậy diện tích mảnh vườn hình chữ nhật là: \(S = a.x = (20 - x)x = - {x^2} + 20x\)
b) Để diện tích mảnh vườn lớn nhất thì S phải lớn nhất:
Ta có \(S = - {x^2} + 20x = - ({x^2} - 20x + 100) + 100 = 100 - {(x - 10)^2} \le 100\)(vì \({(x - 10)^2} \ge 0\))
Diện tích mảnh vườn lớn nhất là 100 \(\left( {{m^2}} \right)\) khi x = 10

Gọi x là chiều rộng của vườn hoa (\(x > 0\), tính bằng đơn vị mét)
Theo giả thiết ta có chiều dài là \(15 - x\)
Diện tích của vườn hoa có phương trình như sau \(f\left( x \right) = x\left( {15 - x} \right) = - {x^2} + 15x\)
Ta có bất phương trình thỏa mãn bài toán như sau:\( - {x^2} + 15x \ge 50 \Leftrightarrow - {x^2} + 15x - 50 \ge 0\)
Xét tam thức \(g\left( x \right) = - {x^2} + 15x - 50\) có hai nghiệm phân biệt là \({x_1} = 5;{x_2} = 10\) và \(a = - 1 < 0\) nên \(g\left( x \right) > 0\) khi x thuộc đoạn \(\left[ {5;10} \right]\)
Vậy khi chiều rộng nằm trong đoạn \(\left[ {5;10} \right]\) mét thì diện tích vườn hoa ít nhất là 50 \({m^2}\).
Diện tích khu đất hình vuông có trồng chè và cà phê là:
3x3=9(km2)
Diện tích trồng chè là:
9:(2+1)x1=3(km2)
Diện tích trồng cà phê là:
9 - 3 = 6 (km2)
Đáp số: 3 (km2)
diện tích khu đất hunhf chữ nhật là:
3.3=9(km2)
diện tích trồng chè là:
9:(2+1)=3(km2)
diện tích trồng cà phê là:
9-3=6(km2)
Đáp số: diện tích trồng chè là 3km2
diện tích trồng cà phê là 6km2