Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi diện tích đáy tháp là S0; diện tích mặt trên của tầng 1; tầng 2; tầng 3; … lần lượt là S1; S2; S3; …; S11.
+ Theo giả thiết diện tích của bề mặt trên mỗi tầng bằng nửa diện tích mặt trên của tầng ngay bên dưới

Vậy diện tích mặt trên của tầng 11 là 6m2.

Chọn A
Diện tích bề mặt của mỗi tầng (kể từ 1) lập thành một cấp số nhân có công bội q = 1 2 và u 1 = 12 288 2 = 6 144.
Khi đó diện tích mặt trên cùng là : u 11 = u 1 q 10 = 6 144 2 10 = 6

Diện tích mặt đáy tháp là u1 = 12 288 (m2).
Diện tích mặt sàn tầng 2 là: u2 = 12 288.\(\frac{1}{2}\) = 6 144 (m2).
...
Gọi diện tích mặt sàn tầng n là un với n ∈ ℕ*.
Dãy (un) lập thành một cấp số nhân là u1 = 12 288 và công bội \(q = \frac{1}{2}\), có số hạng tổng quát là: un = 12 288.\({\left( {\frac{1}{2}} \right)^{n - 1}}\).
Diện tích mặt tháp trên cùng chính là mặt tháp thứ 11 nên ta có:
u11 = 12 288.\({\left( {\frac{1}{2}} \right)^{11 - 1}}\) = 12 (m2).

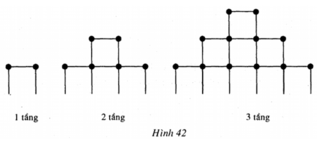
Xây 1 tầng cần 2 que diêm để xếp tầng đế
Xây 2 tầng cần 4 que diêm để xếp tầng đế (4 = 2 + 1.2)
Xây 3 tầng cần 6 que diêm để xếp tầng đế ( 6 = 2 + 2.2)
Xây 100 tầng cần 200 que diêm để xếp tầng đế (200 = 2 + 99.2)

Đáp án D
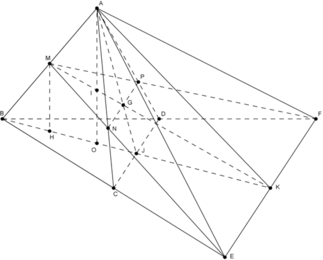
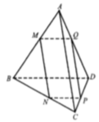
Vẽ AO ⊥ (BCD, MH ⊥ (BCD). Gọi K là trung điểm EF, ta có (ABK) ⊥ (BCD), mp (ABK) chứa AO, MH và là mặt phẳng trung trực của đoạn CD và EF.
Gọi J là trung điểm CD; G là giao điểm của MK và AJ; I là giao điểm của MK và AO.
Gọi N, P lần lượt là giao điểm của ME với AC, MF với AD. Khi đó (MNP) chính là thiết diện khi cắt tứ diện đều ABCD bởi mp (MEF). Vì BE=BF=2a nên ta cũng có MN=MP, hay tam giác MNP cân tại M, đường cao MG.
Để tính diện tích MNP, ta cần đi tìm MG và NP.
Vì G là giao điểm của các đường trung tuyến AJ và MK trong tam giác ABK nên G là trọng tâm của tam giác ABK, do đó MG = 1 3 MK (1) và AG = 2 3 AJ hay NP = 2 3 CD = 2 a 3 (vì NP//CD//EF và chứng minh dựa vào các tam giác đồng dạng, tính chất tỉ số đồng dạng và các đường cao; đường cao AG, AJ trong tam giác ANP và ACD).
Áp dụng nhanh: tam giác đều cạnh a có độ dài mỗi đường cao là 3 2 a (và diện tích là 3 4 a 2 ).
Tam giác đều BCD cạnh a có đường cao BJ = 3 2 a , trọng tâm O, suy ra BO = 2 3 BJ = a 3 . Lại vì MH là đường trung bình trong tam giác vuông ABO nên
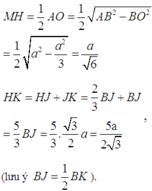
Vì tam giác MHK vuông tại H nên ta có
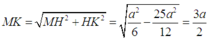
Quay lại (1), ta có
![]()
từ đó tính được diện tích tam giác MNP là
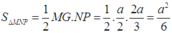

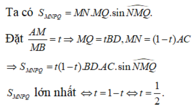
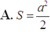


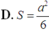
Chọn C
Diện tích bề mặt của tầng 1 là 12288 2 = 6144 m 2
Diện tích mặt trên cùng là: 6144. 1 2 10 = 6 m 2