K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 3 2017
4,(56) =k.1,1(21)
\(\dfrac{452}{99}=k.\dfrac{37}{33}\)
vay \(k=\dfrac{452}{111}\).
V
1
HP
8 tháng 11 2015
\(\frac{a}{5}=\frac{b}{6}=>\frac{a^2}{25}=\frac{b^2}{36}=>\frac{2a^2}{50}=\frac{b^2}{36}\)
áp dụng .... ta có;
\(\frac{2a^2}{50}=\frac{b^2}{36}=\frac{2a^2-b^2}{50-36}=\frac{56}{14}=4\)
từ 2a^2/50=4=>2a^2=200=>a^2=100=>a=+10
b^2/36=4=>b^2=144=>b=+12
vì a;b là 2 số dương >a=10;b=12
khi đó a+b=10+12=22
tick đúng cho tớ nhé
LT
1
3 tháng 1 2017
|x-2,2| =|0,2-x|<=> |x-2,2| -|0,2-x| = 0
|x-2,2|>=0
|0,2-x|>=0
mà |x-2,2|-|0,2-x| =0
hoặc =>x-2,2=0=> x =2
hoặc =>0,2-x=0=> x =0,2
NT
4
TM
25 tháng 12 2016
Vì x;y nguyên nên (2x-3)2 và |y-2| đều là số nguyên
Mà \(\hept{\begin{cases}\left(2x-3\right)^2\ge0\\\left|y-2\right|\ge0\end{cases}}\) nên (2x-3)2 và |y-2| là các số nguyên không âm
TH1: (2x-3)2=0 và |y-2|=1
\(\left(2x-3\right)^2=0\Leftrightarrow2x-3=0\Leftrightarrow2x=3\Leftrightarrow x=\frac{3}{2}\)(loại)
Ta không xét đến |y-2|=1 nữa!
TH2: (2x-3)2=1 và |y-2|=0
- \(\left(2x-3\right)^2=1\Rightarrow\orbr{\begin{cases}2x-3=-1\\2x-3=1\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=-2\\2x=4\end{cases}\Leftrightarrow}}\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
- \(\left|y-2\right|=0\Leftrightarrow y-2=0\Leftrightarrow y=2\)
Vậy có 2 cặp x;y thỏa mãn là .........................
25 tháng 12 2016
\(!y-2!\le1\Rightarrow1\le y\le3\Rightarrow co.the=\left\{1,2,3\right\}\)
\(!2x-3!\le1\Rightarrow1\le x\le2=>x.cothe.=\left\{1,2\right\}\)
Với x=1,2=>có y=2
với 1,3 không có x thỏa mãn
KL:
(xy)=(1,2); (2,2)
18 tháng 9 2023
(1) đúng vì Ot là tia phân giác của góc xOy thì \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy}\)
(2) sai vì
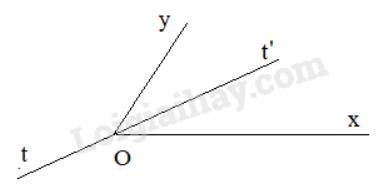
Gọi Ot’ là tia phân giác của góc xOy, ta có: \(\widehat {xOt'} = \widehat {t'Oy}\)
Xét tia Ot là tia đối của tia Ot' thì \(\widehat {xOt'}+ \widehat {xOt}= 180^0; \widehat {t'Oy}+\widehat {tOy}=180^0\) (kề bù)
Ta có: \(\widehat {xOt} = \widehat {tOy}\) nhưng Ot không là tia phân giác của góc xOy.
Chú ý:
Mỗi góc khác góc bẹt chỉ có một tia phân giác.