Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi pit tông đứng yên (trước và sau khi di chuyển) nến áp suất của khí hai bên pti tông là như nhau.
Áp dụng phương trình trạng thái cho khí trong mỗi phần xilanh :
- Phần khí bị nung nóng : $\dfrac{p_0V_0}{T_0}=\dfrac{p_1V_1}{T_1} (1) $
- Phần khí bị làm lạnh : $\dfrac{p_0V_0}{T_0}=\dfrac{p_2V_2}{T_2} (2) $
Từ phương trình $(1),(2)$ và $p_1=p_2\Rightarrow \dfrac{V_1}{T_1}=\dfrac{V_2}{T_2} $
Gọi x là khoảng pit tông dịch chuyển ta có :$\dfrac{(l_0+x)S}{T_1}=\dfrac{(l_0-x)S}{T_2}\Rightarrow x=\dfrac{l_0(T_1-T_2)}{T_1+T_2} $
Thay số ta được $x=2cm$

Pt trạng thái khí :
\(\frac{p_oV_o}{T_o}=\frac{p_1V_1}{T_1}\)
\(\frac{p_oV_o}{T_o}=\frac{p_2V_2}{T_2}\)
Khi xi lanh cân bằng , áp suất ở mỗi phần như nhau và to mỗi phần đều thay đổi đen ta t
=> \(\frac{V_1}{T_1}=\frac{V_2}{T_2}=>\frac{20+2}{300+\Delta t}=\frac{20-2}{300-\Delta t}\)
=>\(\Delta t=30=>T1=330\left(oK\right)\)

Đáp án: A
Gọi hh là chiều cao của bình, yy chiều rộng của bình, xx là khoảng vách ngăn dịch chuyển.
Ta có:
+ Phần A:
- Trạng thái 1: V 0 = h . l 0 y p 0 T 0 = 27 + 273 = 300 K
- Trạng thái 2: V A = h ( l 0 + x ) p A T A = 310 K
+ Phần B:
- Trạng thái 1: V 0 = h . l 0 y p 0 T 0 = 27 + 273 = 300 K
- Trạng thái 2: V B = h ( l 0 − x ) y p B T B = 290 K
Để vách ngăn nằm cân bằng sau khi nung nóng một bên và làm lạnh một bên thì áp suất của phần A và phần B sau khi nung nóng phải bằng nhau:
+ Áp dụng phương trình trạng thái của khí lí tưởng cho mỗi phần ta được:
p 0 V 0 T 0 = p A V A T A (1)
p 0 V 0 T 0 = p B V B T B (2)
Lấy 1 2 ta được: 1 = p A V A T A p B V B T B ⇔ V A V B = T A T B (do p A = p B )
⇔ h l 0 + x y h l 0 − x y = 310 290 ⇔ l 0 + x l 0 − x = 31 29 ⇔ 30 + x 30 − x = 31 29 ⇒ x = 1 c m

Đối với phần khí bị nung nóng:
+ Trạng thái đầu: p 1 ; V 1 = lS; T 1 (1)
+ Trạng thái cuối: p 2 ; V 2 = (l + ∆ l)S; T 2 (2)
Đối với phần khí không bị nung nóng:
+ Trạng thái đầu: p 1 ; V 1 = lS; T 1 (1)
+ Trạng thái cuối: p ' 2 ; V ' 2 = (l - ∆ l)S; T ' 2 = T 1 (2)
Ta có:
p 1 V 1 / T 1 = p 2 V 2 / T 2 = p ' 2 V ' 2 / T 1
Vì pit-tông ở trạng thái cân bằng nên p ' 2 = p 2 . Do đó
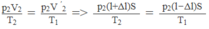
⇒ T 2 = (l + ∆ l/l - ∆ l). T 1
Vậy phải đun nóng khí ở một bên lên thêm ∆ T độ:
![]()
Vì p 1 V 1 / T 1 = p 2 V 2 / T 2 nên:
![]()
Thay số vào ta được:
p 2 ≈ 2,14(atm)

(1) \(t_1=27^0C\rightarrow T_1=300K.\)
V1 = 2l
(2) \(t_1=100^0C\rightarrow T_2=373K.\)
V2 = ?
Do ma sát giữa pittông và xi lanh không đáng kể nên coi áp suất không đổi. Áp dụng định luật Gay luy xac
=>\(\frac{2}{300}=\frac{V_2}{373}\Rightarrow V_3=2,49l\)
=> thể tích của pittong tăng lên là \(\Delta V=0,49l=490cm^3.\)
=> Pit tông được nâng lên một đoạn là \(h=\frac{\Delta V}{S}=\frac{490}{150}=3,26cm=0,326m.\)
cho hỏi các thầy ở trên học 24 nghĩ như thế nào về đáp án này ạ

a) Phần xi lanh bi nung nóng: \(\frac{P_oV_o}{T_o}=\frac{P_1V_1}{T_1}=\frac{P_1V_1}{T_0+\Delta T}\)
Phần xi lanh bị làm lạnh: \(\frac{P_oV_o}{T_o}=\frac{P_2V_2}{T_2}=\frac{P_2V_2}{T_0-\Delta T}\)
Vì P1 = P2 \(\rightarrow\frac{V_1}{V_2}=\frac{T_0+\Delta T}{T_0-\Delta T}\) (1)
Gọi đoạn di chuyển của pit-tông là x, ta có: V1 = (l + x)S và V2 = (l - x)S (2)
Từ (1) và (2) ta có \(\frac{\left(l+x\right)S}{\left(l-x\right)S}=\frac{T_0+\Delta T}{T_0-\Delta T}\rightarrow\) x = \(\frac{l\Delta T}{T_0}\)
b) P2V2 = P0V \(\rightarrow\) P2 = P0V0 /(l - x)S (1)
P1V1 = P0V \(\rightarrow\) P2 = P0V0/(l + x)S (2)
Xét pit-tông: F2 - F1 = ma \(\rightarrow\) (P2 - P1)S = ma (3)
Từ (1), (2), và (3)
\(\left(\frac{P_0V}{S\left(l-r\right)}\right)-\left(\frac{P_0V}{S\left(l+r\right)}\right)S\)= ma \(\rightarrow\) a = 2P0V0x/(l2 – x2)m

T1=27+10+273=310K
T2=27-10+273=290K
phương trình trạng thái đối với phần khí bị nung nóng
\(\frac{p_0.V_0}{T_0}=\frac{p_1.V_1}{T_1}\)
phương trình trạng thái đối với phần khí bị làm lạnh
\(\frac{p_0.V_0}{T_0}=\frac{p_2.V_2}{T_2}\)
đẳng áp: \(p_1=p_2\)
\(\Rightarrow\frac{V_1}{T_1}=\frac{V_2}{T_2}\)
gọi x là đoạn bị dịch chuyển
\(\Leftrightarrow\frac{\left(l_0+x\right).S}{T_1}=\frac{\left(l_0-x\right).S}{T_2}\)
\(\Rightarrow x=\)1cm
Thanks