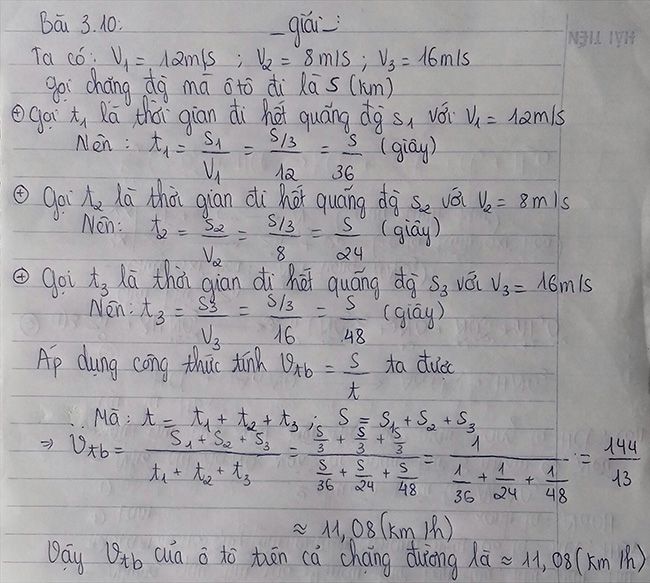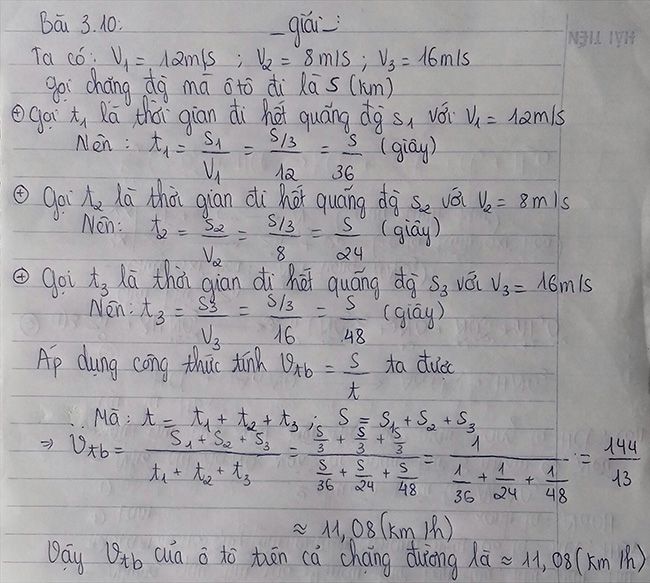Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có CT tính vạn tốc trung bình là:
Vtb = AB/(t1+t2+...+tn)
Với 1/4 quãng đường đầu người đó đi hết thời gian là:
t1 = AB/(4.V1) (1)
Quãng đường còn lại 3AB/4 mà nửa thời gian còn lại cũng tức là nửa quãng đường còn lại người đó đi hết thời gian là:
t2 = 3AB/(8.V2) (2)
Quãng đường còn lại là 3AB/8 mà người đó đi nửa quãng đường còn lại với vận tốc V1 nên thời gian người đó đi hết là:
t3 = 3AB/(16.V1) (3)
Quãng đường còn lại là AB - AB/4 - 3AB/8 - 3AB/16 3AB/16 người đó đi hết:
t4 = 3AB/(16.V2) (4)
=> t1+t2+t3+t4 = (1) +(2) +(3) +(4)
Bạn + vào quy đồng lên là được kết quả sau:
= (7AB.V2 +9AB.V1)/(16.V1.V2)
= AB(9V1 +7V2)/(16V1.V2)
=> AB/(t1+t2+t3+t4) = AB/[AB(9V1 +7V2)/(16V1.V2)]
= (AB.16V1.V2)/[AB.(9V1 +7V2)
= 16V1.V2/(9V1 +7V2)
=> Vận tốc trung bình của người đó là:
Vtb = 16V1.V2/(9V1 +7V2)
gọi AB là s
, thời gian đi với v1= (s/2)/t1 => t1 = s/2v1
thời gian đi với v2 = ( s/2):2/t2 => t2 = s/4v2
..........................v3 = s - s/2)- s/4 )/t3 => t3 = s/4v3
vậy vtb= (s/2 + s/4 +s/4)/ (t1 +t2+t3) = 1/(1/2v1 + 1/ 4v2 + 1/4v3)

(lần sau ghi cs dấu vào nha bn)
Do quãng đường được chia làm 2 đoạn nên \(\dfrac{s}{2}\)
Thời gian ng` ấy ik quãng đường đầu:
\(t_1=\dfrac{s}{2v_1}\left(h\right)\left(1\right)\)
Thời gian ng` ấy ik quãng đường còn lại:
\(t_2=\dfrac{s}{2v_2}\left(h\right)\left(2\right)\)
Từ (1) và (2). Thời gian mà ng` ấy ik cả quãng đường:
\(t_{qd}=\dfrac{s\left(v_1+v_2\right)}{2.v_1.v_2}\)
Vận tốc trung bình ng` ấy ik cả quãng đường:
\(v_{tb}=8=\dfrac{s}{\dfrac{s\left(v_1+v_2\right)}{2v_1.v_2}}=\dfrac{v_1+v_2}{2.12.v_2}=\dfrac{12+v_2}{24v_2}\left(km/h\right)\)
\(v_{tb}=\dfrac{12+v_2}{24v_2}=8\Rightarrow12+v_2=3v_2\Rightarrow v_2=6\left(km/h\right)\)
Vậy ...
Gọi quãng đường là s = > nửa quãng đường là s / 2
Thời gian ng đo đi trong nửa quãng đường đầu là :
t1 = s / 2 : v1 =s / 2 : 12 = s / 24
Thời gian người đó đi trong nửa quãng đường sau là :
t2 = s / 2 : v2 = s / 2 : 20 = s / 40
Vận tốc tb người đo đi trong cả quãng đường là :
Vtb = s/t = (s1+ s2) / ( t1+t2 ) = s / ( s / 24 + s / 40 ) = s / [s*(1/24 + 1/40 )]
< = > Vtb= 1 : (1/24 + 1/20)
< = > Vtb= 15 (km/h )
Vậy vận tốc trung bình của người đo trên cả quãng đường là 15 km/h

chắc bạn học lý nên cũng biết nếu hai đoạn đường bằng nhau thì ta có công thức
vtb=2.v1.vtb'/(v1+vtb')
trong đó vtb' là vân tốc trung bình của nửa đoạn đường sau
theo đề bài thì vtb'=(s2+s3)/(t2+t3)
vtb'=(v2.t2+v3.t3)/(t2+t3)
do t2=t3 nên
vtb'=t2(v2+v3)/2t2
vtb'=(v2+v3)/2
thế vào pt trên kia được vtb=2v1(v2+v3)/(2v1+v2+v3)
copy thì cũng biết bỏ phần đầu đi chứ ko thấy nó rất nhàm à

vì ôtô đi trên chặng đường gồm 3 đoạn liên tiếp cùng chiều dài nên suy ra S1=S2=S3=\(\dfrac{S}{3}\)(m)
thời gian người đó đi trên đoạn đường đầu là
\(t_1=\dfrac{S_1}{V_1}=\dfrac{\dfrac{S}{3}}{16}=\dfrac{S}{48}\) (s)
thời gian oto đó đi trên đoạn đường thứ 2 là
\(t_2=\dfrac{S_2}{V_2}=\dfrac{S}{\dfrac{3}{10}}=\dfrac{S}{30}\) (s)
thời gian oto đó đi trên đoạn đường thứ 3 là
\(t_3=\dfrac{S_3}{V_3}=\dfrac{S}{\dfrac{3}{20}}=\dfrac{S}{60}\) (s)
vận tốc trung bình của oto trên cả quãng đường là
\(V_{tb}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{\dfrac{1}{3}S+\dfrac{1}{3}S+\dfrac{1}{3}S}{\dfrac{S}{48}+\dfrac{S}{30}+\dfrac{S}{60}}=\dfrac{\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}}{\dfrac{1}{48}+\dfrac{1}{30}+\dfrac{1}{60}}=14,11\left(m\right)\)

Vì ô tô chuyển động trên chặng đường gồn 3 đoạn bằng nhau
\(\Leftrightarrow s_1=s_2=s_3=\dfrac{s}{3}\)
Thời gian ô tô chuyển động trên quãng đường thứ nhất là :
\(t_1=\dfrac{s_1}{v_1}=\dfrac{\dfrac{s}{3}}{12}=\dfrac{s}{36}\left(h\right)\)
Thời gian ô tô chuyển động trên quãng đường thứ hai là :
\(t_2=\dfrac{s_2}{v_2}=\dfrac{\dfrac{s}{3}}{8}=\dfrac{s}{24}\left(h\right)\)
Thời gian ô tô chuyển động trên quãng đường thứ ba là :
\(t_3=\dfrac{s_3}{v_3}=\dfrac{\dfrac{s}{3}}{16}=\dfrac{s}{48}\left(h\right)\)
Vận tốc trung bình của ô tô trên cả chặng đường đó là :
\(v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{\dfrac{s}{3}+\dfrac{s}{3}+\dfrac{s}{3}}{\dfrac{s}{36}+\dfrac{s}{24}+\dfrac{s}{48}}=\dfrac{s\left(\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}\right)}{s\left(\dfrac{1}{36}+\dfrac{1}{24}+\dfrac{1}{48}\right)}=11\left(h\right)\)
Vậy..

ta có:
thời gian nhười đó đi trong nửa quãng đường đầu là:
\(t_1=\frac{S_1}{v_1}=\frac{S}{2v_1}=\frac{S}{80}\left(1\right)\)
vận tốc trung bình của người đó là:
\(v_{tb}=\frac{S_1+S_2+S_3}{t_1+t_2+t_3}=\frac{S}{t_1+t'}\left(3\right)\)
ta lại có:
S2+S3=S/2
\(\Leftrightarrow t_2v_2+t_3v_3=\frac{S}{2}\)
\(\Leftrightarrow45t_2+35t_3=\frac{S}{2}\)
\(\Leftrightarrow\frac{45t'}{2}+\frac{35t'}{2}=\frac{S}{2}\)
\(\Leftrightarrow70t'=S\)
\(\Rightarrow t'=\frac{S}{70}\left(2\right)\)
đem (1) và (2) thế vào phương trình (3) ta có:
\(v_{tb}=\frac{S}{\frac{S}{80}+\frac{S}{70}}=\frac{S}{S\left(\frac{1}{80}+\frac{1}{70}\right)}=\frac{1}{\frac{1}{80}+\frac{1}{70}}\)
từ đó ta suy ra vtb=37,3km/h
\(\Rightarrow S=v_{tb}.t=74,6km\)