Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ban tu ve hinh nhe? :D
Hệ kín động lượng được bảo toàn. \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Ta có: \(\left\{{}\begin{matrix}p=mv=250m\left(kg.m/s\right)\\p_1=\dfrac{m}{2}.v_1=125m\left(kg.m/s\right)\end{matrix}\right.\)
Áp dụng định lý hàm cos ta có:
\(\cos\alpha=\dfrac{p^2+p_1^2-p_2^2}{2p_1p}=\dfrac{250^2m^2+125^2m^2-\dfrac{m^2}{4}v_2^2}{2.250m.125m}\)
\(\Leftrightarrow250.125=250^2+125^2-\dfrac{1}{4}v_2^2\) \(\Rightarrow v_2=\sqrt{187500}\left(m/s\right)\simeq433\left(m/s\right)\)
Gọi \(\beta\) là góc hợp bởi mảnh 2 và phương thẳng đứng:
\(\cos\beta=\dfrac{p^2+p_2^2-p_1^2}{2p_2p}=\dfrac{250^2+216,5^2-125^2}{2.250.216,5}=0,86\)
\(\Rightarrow\beta\simeq31^0\)

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
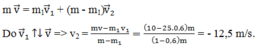
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Lời giải
Ta có:
+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
+ Gọi m 1 = 0 , 6 m là khối lượng của mảnh thứ nhất
=> Khối lượng của mảnh còn lại là m 2 = m − m 1 = m − 0 , 6 m = 0 , 4 m
+ Áp dụng định luật bảo toàn động lượng ta có: p → = p → 1 + p → 2
m v → = m 1 v → 1 + m − m 1 v → 2
Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ
=> v → 1 ↑ ↑ v →
Ta suy ra:
v 2 = m v − m 1 v 1 m − m 1 = ( 10 − 25.0 , 6 ) m ( 1 − 0 , 6 ) m = − 12 , 5 m / s
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Đáp án: B

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
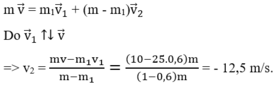
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

a) Áp dụng định luật bảo toàn động lượng:
chiều (+) là chiều chuyển động của đạn:
\(0=Mv+mv_0\Rightarrow v=-4\left(m/s\right)\)
=> khẩu pháo chuyển động ngược chiều đạn bay.
b) \(MV=Mv+mv_o\Rightarrow v=1\left(m/s\right)\)
=> Khẩu pháo chuyển động cùng chiều đạn bay.
c) \(-MV=Mv+mv_o\Rightarrow v=-9\left(m/s\right)\)
=> Khẩu pháo chuyển động ngược chiều đạn bay.
Chú thích: V là vận tốc khẩu pháo trước bắn. v là vận tốc khẩu pháo sau bắn và vo là vận tốc viên đạn khi ra khỏi nòng pháo.
b,c của cậu sai r kìa !!! lúc chưa bắn phải cộng thêm khối lượng của viên đạn nữa :))

p1 = m1v1 = 1.3 = 3kg.m/s
p2 = m2v2 = 3.1 = 3kg.m/s
a) Động lượng của hệ: =
1 +
2
Độ lớn của hệ: p = p1 + p2 = 3 + 3 = 6kg.m/s
b) Động lượng của hệ: =
1 +
2
Độ lớn của hệ: p = | p1 - p2 | = | 3 - 3 | = 0kg.m/s
c) Động lượng của hệ: =
1 +
2
Độ lớn của hệ: \(p=\sqrt{p^2_1+p_2^2}=\sqrt{3^2+3^2}=4,242kg.m/s\)
d) Động lượng của hệ: =
1 +
2
Độ lớn của hệ: p = p1 = p2 = 3kg.m/s

Chọn C.
Ta có: v 2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
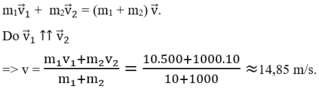

Chọn C.
Ta có: v2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
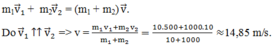
mặc định mảnh nhỏ là m1 còn mảnh to là m2 nhé
a) Áp dụng định lý hàm cos:
\(p_2^2=p_1^2+p^2-2p_1p\cos\left(p_1;p\right)\)
\(\Rightarrow p_2=\sqrt{p_1^2+p^2-2p_1p\cos\left(p_1;p\right)}=....\Rightarrow v_2=\dfrac{p_2}{m_2}\) Thay số vào nốt là xong bạn
\(\cos\left(p_2;p\right)=\dfrac{p_2^2+p^2-p_1^2}{2p_2p}=.....\)
b) Mảnh nhỏ bay lên theo phương thẳng đứng cho ta hình dạng của 1 tam giác vuông
\(p_2=\sqrt{p^2+p_1^2}=\sqrt{\left(mv\right)^2+\left(m_1v_1\right)^2}=...\) \(\Rightarrow v_2=\dfrac{p_2}{m_2}=.....\) (....bạn tự tính điền vào )
\(\cos\left(p_2;p\right)=\dfrac{p}{p_2}=......\) tính nốt :D