Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
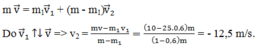
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Lời giải
Ta có:
+ Hệ viên đạn ( hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
+ Gọi m 1 = 0 , 6 m là khối lượng của mảnh thứ nhất
=> Khối lượng của mảnh còn lại là m 2 = m − m 1 = m − 0 , 6 m = 0 , 4 m
+ Áp dụng định luật bảo toàn động lượng ta có: p → = p → 1 + p → 2
m v → = m 1 v → 1 + m − m 1 v → 2
Theo đầu bài, ta có mảnh 1 tiếp tục bay theo hướng cũ
=> v → 1 ↑ ↑ v →
Ta suy ra:
v 2 = m v − m 1 v 1 m − m 1 = ( 10 − 25.0 , 6 ) m ( 1 − 0 , 6 ) m = − 12 , 5 m / s
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.
Đáp án: B

Chọn B.
Hệ viên đạn (hai mảnh đạn) ngay khi nổ là một hệ kín nên động lượng hệ được bảo toàn
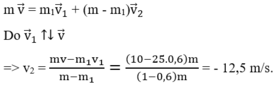
Dấu (-) chứng tỏ mảnh đạn thứ 2 sẽ chuyển động ngược chiều chuyển động ban đầu của viên đạn và mảnh đạn thứ nhất.

Ban tu ve hinh nhe? :D
Hệ kín động lượng được bảo toàn. \(\overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}\)
Ta có: \(\left\{{}\begin{matrix}p=mv=250m\left(kg.m/s\right)\\p_1=\dfrac{m}{2}.v_1=125m\left(kg.m/s\right)\end{matrix}\right.\)
Áp dụng định lý hàm cos ta có:
\(\cos\alpha=\dfrac{p^2+p_1^2-p_2^2}{2p_1p}=\dfrac{250^2m^2+125^2m^2-\dfrac{m^2}{4}v_2^2}{2.250m.125m}\)
\(\Leftrightarrow250.125=250^2+125^2-\dfrac{1}{4}v_2^2\) \(\Rightarrow v_2=\sqrt{187500}\left(m/s\right)\simeq433\left(m/s\right)\)
Gọi \(\beta\) là góc hợp bởi mảnh 2 và phương thẳng đứng:
\(\cos\beta=\dfrac{p^2+p_2^2-p_1^2}{2p_2p}=\dfrac{250^2+216,5^2-125^2}{2.250.216,5}=0,86\)
\(\Rightarrow\beta\simeq31^0\)

Chọn C.
Ta có: v2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
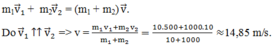

Chọn C.
Ta có: v 2 = 36 km/h = 10 m/s.
Va chạm giữa viên đạn và toa xe là va chạm mềm nên động lượng của hệ (đạn + xe) là không đổi:
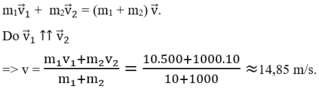

Chọn A.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua mọi ma sát, cơ năng của con lắc được bảo toàn: W 1 = W 2 = W đ m a x
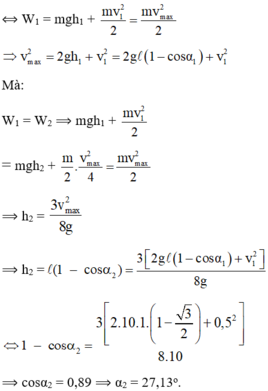

Chọn A.
Chọn mốc thế năng tại vị trí cân bằng của con lắc.
Bỏ qua mọi ma sát, cơ năng của con lắc được bảo toàn: W1 = W2 = Wđmax
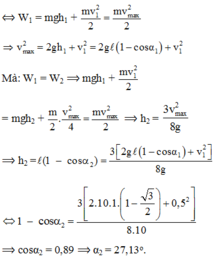

C.
Chọn chiều dương hướng lên, gốc tọa độ y = 0 là ví trí ném, gốc thời gian t = 0 là lúc ném.
Ta có: t = 0, v0 = 30m/s. a = - g = - 10 m/s2.
Suy ra vận tốc của vật tại thời điểm t: v = v0 – gt = 30 – 10t
⟹ lúc t = 4s, v = - 10 m/s < 0, chứng tỏ khi đó vật chuyển động ngược chiều dương tức là đang rơi xuống.