Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biên độ tổng hợp: \(A^2=7^2+8^2+2.7.8.\cos(\pi/3)=169\)
\(\Rightarrow A = 13 (cm)\)
Áp dụng công thức độc lập: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 13^2=12^2+\dfrac{v^2}{(20\pi)^2}\)
\(\Rightarrow v = 100\pi(cm/s)\)

Đáp án A
Phương pháp: áp dụng công thức tính biên độ của dao động tổng hợp hai dao động cùng phương, cùng tần số
Cách giải:
Biên độ dao động tổng hợp: A 2 = A 1 2 + A 2 2 + 2 A 1 A 2 cos ∆ φ ⇒ A = 7 cm

Chọn đáp án D
Tại t: dao động thứ hai có vận tốc là:
− 20 π 3 c m / s = − V 2 max 2 . 3 cm/s
và tốc độ đang giảm nên tại t pha dao động thứ 2 là 2π/3 rad.
Mà x1 và x2 lệch pha nhau π/3 suy ra tại t thì pha của x1 là π/3.
Suy ra A 1 = 3.2 = 6 cm.
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos φ = 6 2 + 10 2 + 2.6.10. cos π 3 = 14 c m
Suy ra khi pha dao động tổng hợp là − 2 π 3 thì li độ dao động tổng hợp là:
x = A . cos − 2 π 3 = − 7 c m .

+ Ta có
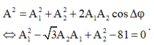
Để phương trình trên tồn tại nghiệm A 1 thì
![]()
Thay giá trị A 2 vào phương trình đầu, ta tìm được
![]()
Đáp an A
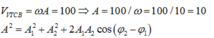
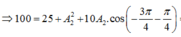
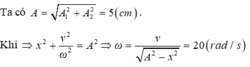
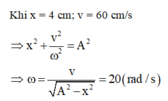
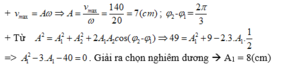
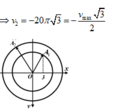
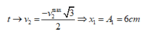
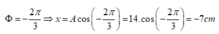
Chọn A
+ Dao động tổng hợp A = A 1 2 + A 2 2 + 2 A 1 A 2 cos ( φ 2 - φ 1 ) = 49 + 94 + 2 . 7 . 8 . 0 , 5 = 13 ( c m )
+ Áp dụng ( x A ) 2 + ( v A w ) 2 = 1 ⇒ v = w A 2 - x 2 = 20 π 13 2 - 12 2 = 314 cm / s