Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lực kéo về tác dụng lên vật có độ lớn cực đại là \(F_{max}=kA= m(2\pi f)^2 A = 0,1.4.10.5^2.0,04 = 4N.\)

Đáp án B
Phương pháp: Áp dụng công thức tính lực kéo về
Cách giải:
Tần số góc: ω = 2πf = 10π (rad/s)
Ta có độ lớn lực kéo về F = k x
=> Lực kéo về có độ lớn cực đại :
![]()
=> Chọn B

+ Ta có: Fkmax = mga0 = 0,05 ® a0 = 0,1 rad
+ W t = 1 2 W d → W = 3 Wt = 3mgl(1- cosa)
+ Áp dụng bảo toàn cơ năng ta được: 3mgl(1 - cosa) = mgl(1 - cosa0)
cos α = 2 + cos α 0 3
+ T = mg(3cosa - 2cosa0) = 0,5025 N
ü Đáp án B

D Đáp án B
+ Ta có: Fkmax = mga0 = 0,05 ® a0 = 0,1 rad
+ W t = 1 2 W d => W = 3 Wt = 3mgl(1- cosa)
+ Áp dụng bảo toàn cơ năng ta được: 3mgl(1 - cosa) = mgl(1 - cosa0)
→ cos α = 2 + cos α 0 3
+ T = mg(3cosa - 2cosa0) = 0,5025 N

Lực kéo về
\(F = -kx= -k.A.\cos (\omega t +\varphi)\)
So sánh với phương trình \(F=-0.8\cos 4t(N)\) => \(\omega = 4\)(rad/s) và \( k.A = 0,8 \)
\(=> m\omega^2 A = 0,8 => A = \frac{0,8}{m\omega^2}= \frac{0,8}{0,5.4^2}= 0,1 m = 10cm.\)
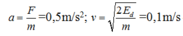



Đáp án C