Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
+ Theo định luật bảo toàn năng lượng: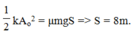
+ Độ giảm biên độ sau nửa chu kì: 
+ Sau thời gian t biên độ của vật giảm hết thì vật thực hiện được n dao động:
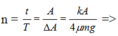
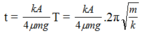
=> Tốc độ trung bình: vtb = S : t = 4,026 m/s.

Chọn đáp án B
+ Sau 10 dao động vật dừng lại như vậy có 20 lần qua VTCB
+ Độ giảm biên độ của vật sau một lần qua VTCB:
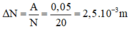
Mặt khác vật dao động tắt dần trên mặt phẳng nghiên nên ta có độ giảm biên độ sau một lần vật qua VTCB:
![]()

Đáp án C
Tốc độ trung bình trong cả quá trình dao động tắt dần:
![]()

Chọn đáp án B.
Do không thay đổi về k, m => ω không đổi.
→ ω = k m = 20 0 , 2 = 10 π ( r a d / s ) .
Ta có năng lượng truyền cho vật là:
E t r u y e n = 1 2 m v 2 = 1 2 .0 , 2.1 2 = 0 , 1 ( J )
⇒ 1 2 k A 2 = E t r u y e n = 0 , 1 ⇒ A = 0 , 1 ( m )
Khi tới biên A lần đầu, năng lượng còn lại là:
![]()
![]()
=> Biên độ còn lại:
![]()

Hướng dẫn:
+ Độ biến dạng của lò xo tại vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 1.10 100 = 10 − 3 m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên A 1 = X 0 – x 0 .
Cứ sau mỗi nửa chu kì, kể từ nửa chu kì thứ 2 biên độ của vật dao động so với các vị trí cân bằng tạm sẽ giảm 2 x 0 .
→ Ta xét tỉ số A 1 2 x 0 = X 0 − x 0 2 x 0 = 0 , 1 − 10 − 3 2.10 − 3 = 49 , 5
→ Biên độ của vật sau 49 nửa chu kì tiếp theo là A 49 = A 1 – ( 49 . 2 + 1 ) x 0 = 1 m m → vật tắt dần tại đúng vị trí lò xo không biến dạng.
+ Áp dụng định luật bảo toàn và chuyển hóa năng lượng ta có 1 2 k X 0 2 = μ m g S → S = k X 0 2 2 μ m g = 100.0 , 1 2 2.0 , 1.0 , 1.10 = 5 m
Đáp án B
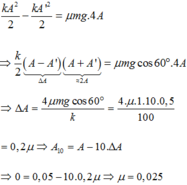


Trong trường hợp này chỉ có duy nhất một sự khác biệt: Ở vị trí cân bằng mới, vật cách VTCB cũ là x0 thì:
\(kx_0=\mu N=\mu mg\cos60^0\Leftrightarrow x_0=\frac{\mu mg\cos60^0}{k}\)
Độ giảm biên độ sau mỗi chu kì là: \(4x_0=\frac{4\mu mg\cos60^0}{k}\)
Bài này không có m và k nên theo gợi ý này bạn làm tiếp nhé.