Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
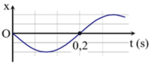
Phương pháp: Sử dụng công thức ω = 2π/T kết hợp k năng đọc đồ thị.
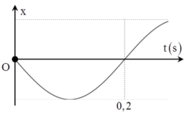
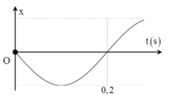
Cách giải: Nhìn vào đồ thị ta thấy T/2 = 0,2s = T = 0,4s = ω = 5π (rad/s)

+ Ban đầu vật đi qua vị trí cân bằng theo chiều âm, vậy pha ban đầu của dao động là 0,5π rad.
ü Đáp án A

Chọn đáp án B
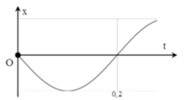
Dựa vào hình vẽ ta có:
T 2 = 0 , 2 s ⇒ T = 0 , 4 s
⇒ ω = 2 π T = 5 π r a d / s .

Ban đầu vật đi qua vị trí cân bằng theo chiều âm → φ0 = 0,5π
Đáp án D

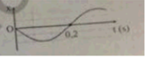
Theo đồ thị, ta dễ dàng thấy được ban đầu khi t = 0, vật đang ở biên âm \(\Rightarrow\varphi=\pi\)
Thời gian để vật đi từ biên âm đến VTCB là \(\dfrac{T}{4}\)
\(\Rightarrow\dfrac{T}{4}=1\Rightarrow T=4\left(s\right)\Rightarrow\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\)
Vậy phương trình dao động của vật là: \(x=Acos\left(\omega t+\varphi\right)=4cos\left(\dfrac{\pi}{2}t+\pi\right)\left(cm\right)\)

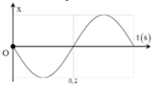
+ Đồ thị biễu diễn sự biến thiên của gia tốc theo li độ x có dạng là một đoạn thẳng.
Đáp án C
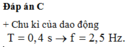
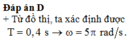

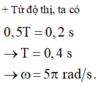
Chọn đáp án B.
Ta có: a = − ω 2 x (a phụ tuộc vào x giống dạng y = ax) nên có đồ thị đoạn thẳng đi qua gốc tọa độ; x dương thì a âm và ngược lại.