Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu kì: T = 0,2s.
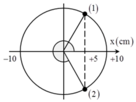
Biểu diễn dao động bằng véc tơ quay ta có:
Pha ban đầu bằng 0 nên véc tơ quay xuất phát từ M.
Chất điểm qua li độ 5cm theo chiều dương ứng với véc tơ quay qua N.
Khi véc tơ quay quay được 2009 vòng, nó qua N 2009 lần, ứng với dao động qua 5cm theo chiều dương 2009 lần. Tuy nhiên ở vòng quay cuối, chỉ cần quay đến N là đủ.
Vậy thời gian cần thiết là: t = \(2009T - \frac{60}{360}T = (2008+\frac{5}{6}).0,2=401,77\)s

Chu kì T = 0,2 s.
Biểu diễn bằng véc tơ quay ta được
Do pha ban đầu bằng 0 nên véc tơ quay xuất phát từ M. Véc tơ quay quay được 1004 vòng thì hình chiếu qua li độ 5cm là 2008 lần, nhưng do vòng quay cuối chỉ cần đến N là đủ, nên thời gian cần thiết là: t = 1004T - \(\frac{60}{360}\)T = (1003 + \(\frac{5}{6}\)).0,2 = 200,77s.

Thời điểm thứ hai vật đi qua li độ `x=5 cm` là: `\Delta t=[3T]/4+T/12=[5T]/6 (s)`
Thời điểm vật đi qua vị trí có li độ `x=5 cm` lần thứ `2008` là:
`t=[5T]/6+[2008-2]/2 T=6023/6 T=6023/6 . [2\pi]/[10\pi]=6023/30~~200,8(s)`.

+ Tại t = 0 vật đang ở vị trí biên dương.
Trong một chu kì vật đi qua vị trí x = 5 cm hai lần → ta tách 2008 = 2006 + 2.
+ Tổng thời gian thoãn mãn yêu cầu bài toán là:
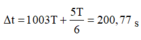
Đáp án A

\(t=0,4s\)
\(t=0\Rightarrow x=10=A\)
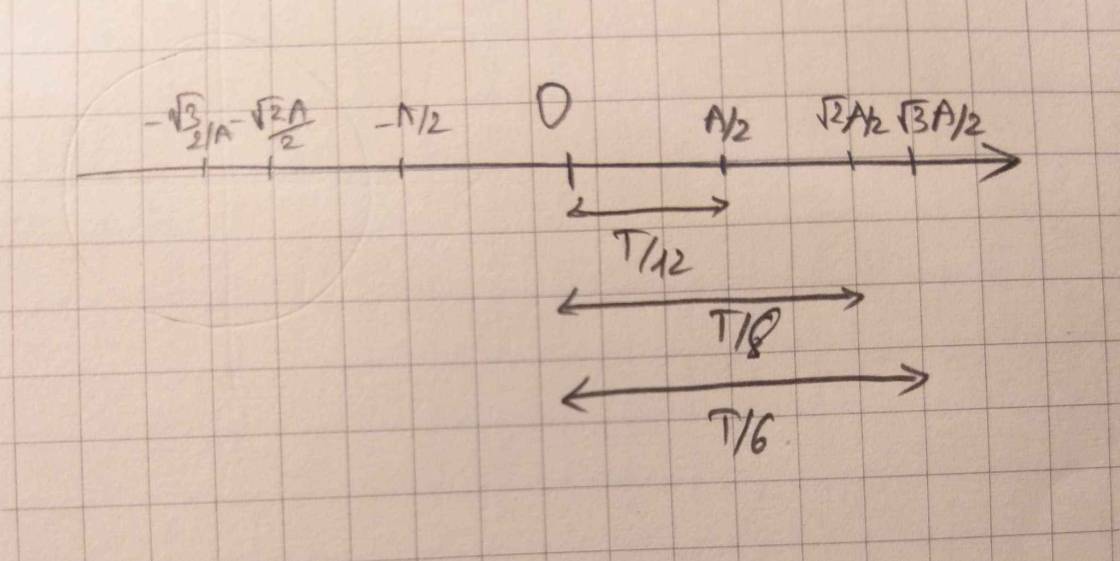
Thời điểm vật qua vị trí \(x=5=\frac{A}{2}\)
Vì trong một chu kỳ vật đi qua vị trí x=5 lần nên :
\(t=\frac{2008}{2}=1003.2+2=1003T+t'\)
Vẽ trục ngang ra tìm t'\(\Rightarrow t'=\frac{T}{2}+\frac{T}{4}+\frac{T}{12}\)Vậy : t' = 2003T + 5T/6 = 6023T/6 = 401,53 (s)
Đáp án A
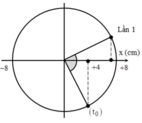
+ Tại thời điểm t = 0 vật đi qua vị trí x = 4 cm theo chiều dương.
Trong mỗi chu kì vật đi qua vị trí x = 4 3 cm theo chiều âm 1 lần → Ta tách 2017 = 2016 + 1.
+ Biểu diễn các vị trị tương ứng trên đường tròn, từ hình vẽ. Ta có:
Δt = 2016T + 0,25T = 2016,25 s


Chu kì: T = 0,2s.
Biểu diễn dao động bằng véc tơ quay ta có:
Do pha ban đầu bằng 0 nên véc tơ quay xuất phát từ M.
Chất điểm qua li độ 5cm theo chiều âm nên véc tơ quay qua điểm N.
Như vậy, véc tơ quay quay được 999 vòng thì nó qua N 999 lần. Trong lần cuối cùng chỉ cần qua tiếp từ M đến N là đủ.
Vậy tổng thời gian cần thiết là: \(999T + \frac{60}{360} T=(999+\frac{1}{6}).0,2=199,833\)s