Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`@W_t=mgz=2.10.2=40(J)`
`W_đ=1/2mv^2=1/2 .2.0^2=0(J)`
`W=W_t+W_đ=40+0=40(J)`
`@W_[(W_đ=2W_t)]=W_[đ(W_đ=2W_t)]+W_[t(W_đ=2W_t)]=40`
Mà `W_[đ(W_đ=2W_t)]=2W_[t(W_đ=2W_t)]`
`=>3W_[t(W_đ=2W_t)]=40`
`<=>3mgz_[(W_đ=2W_t)]=40`
`<=>3.2.10.z_[(W_đ=2W_t)]=40`
`<=>z_[(W_đ=2W_t)]~~0,67(m)`
`@W_[đ(max)]=W_[t(max)]=40`
`<=>1/2mv_[max] ^2=40`
`<=>1/2 .2v_[max] ^2=40`
`<=>v_[max]=2\sqrt{10}(m//s)`
Sao lại 3 lần thế năng? Trong khi đó có 2? giải thích giúp em.

Tóm tắt m=1kg; hA=16m; g=10m/s2
a,Xét tại điểm A
Động năng của vật : \(W_{đA}=0J\)
Thế năng của vật:\(W_{tA}=mgh_A=160J\)
Cơ năng của vật: \(W=W_{đA} +W_{tA}=160J\)
b, Gọi B là điểm mà vật có động năng bằng 2 lần thế năng
\(\Rightarrow W_{đB}=2W_{tB}\)
Vì vật chỉ chịu tác dụng của trọng lực < Đề thiếu dữ kiện " Bỏ qua ma sát">
nên cơ năng được bảo toàn
\(\Rightarrow W_B=W_A=160J\)
Xét điểm B
Độ cao của vật so với mặt đất lúc này
\(W_B=W_{đB}+W_{tB}\Leftrightarrow W_B=3W_{tB}\Leftrightarrow W_B=3mgh_B\)
\(\Rightarrow h_B=\dfrac{W_B}{3mg}=\dfrac{16}{3}m\)

a. Thế năng của vật tại vị trí thả:
\(W_t=mgh=0,1\cdot10\cdot45=45\left(J\right)\)
Cơ năng của vật:
\(W=W_t+W_d=45+\dfrac{1}{2}\cdot 0,1\cdot0^2=45\left(J\right)\)
b. Ta có định luật bảo toàn cơ năng: \(W_A=W_B\)
\(\Leftrightarrow45=\dfrac{1}{2}\cdot0,1\cdot v_B^2+0\cdot10\cdot0,1\)
\(\Leftrightarrow v_B=30\left(\dfrac{m}{s}\right)\)
\(\Rightarrow W_{d_B}=\dfrac{1}{2}\cdot0,1\cdot30=45\left(J\right)\)

chọn mốc thế năng tại mặt đất:
Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn:
a) \(W_1=W_2\Leftrightarrow mgz_1=\dfrac{1}{2}mv_2^2\Rightarrow v_2=.....\) ( Bảo toàn tại vị trí thả và mặt đất )
b) \(W_1=W_3\Leftrightarrow mgz_1=3mgz_3\Rightarrow z_3=......\)
c) \(W_1=W_4\Leftrightarrow mgz_1=\dfrac{3}{2}.\dfrac{1}{2}mv_4^2\Rightarrow v_4=......\)
d) Khi m 0,5kg ta có: Cơ năng luôn được bảo toàn \(W=W_đ+W_t=\dfrac{1}{2}mv_1^2+mgz_1=0+mgz_1=.....\)
Mấy cái dấu..... bạn tự thế số vào tính nốt hộ mình nha

a)Cơ năng tại vị trí thả vật:
\(W=\dfrac{1}{2}mv^2+mgz=2\cdot10\cdot2=40J\)
b)Vận tốc vật khi chạm đất:
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot2}=2\sqrt{10}\)m/s
c)Cơ năng tại nơi \(W_t=2W_đ\Rightarrow W_đ=\dfrac{1}{2}W_t\):
\(W_1=W_đ+W_t=\dfrac{1}{2}W_t+W_t=\dfrac{3}{2}W_t=\dfrac{3}{2}mgz\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow40=\dfrac{3}{2}mgz\Rightarrow z=\dfrac{4}{3}m\)
d)Cơ năng tại nơi \(W_đ=3W_t\Rightarrow W_t=\dfrac{1}{3}W_đ\):
\(W_2=W_đ+W_t=\dfrac{4}{3}W_đ=\dfrac{2}{3}mv^2\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow40=\dfrac{2}{3}mv^2\Rightarrow v=\sqrt{30}\)m/s

Chọn thế năng tại mặt đất
`a)W=W_đ+W_t=1/2mv^2+mgz=1/2 . 0,2,4^2+0,2.10.5=11,6(J)`
`b)W=W_[t(max)]=11,6`
`<=>mgz_[max]=11,6`
`<=>0,2.10.z_[max]=11,6`
`<=>z_[max]=5,8(m)`
`c)W_(W_đ=2W_t)=W_[đ(W_đ=2W_t)]+W_[t(W_đ=2W_t)]=11,6`
Mà `W_[đ(W_đ=2W_t)]=2W_[t(W_đ=2W_t)]`
`=>3W_[t(W_đ=2W_t)]=11,6`
`<=>3mgz_(W_đ=2W_t)=11,6`
`<=>3.0,2.z_(W_đ=2W_t)=11,6`
`<=>z_(W_đ=2W_t)~~19,3(m)`

Chọn gốc tính thế năng ( Z0 = 0) tại mặt đất.
Vận tốc của vật sau khi rơi được quãng đường
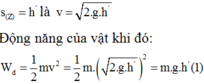
Thế năng của vật tương ứng với vị trí đó bằng:
![]()
IXét tổng quát tại vị trí động năng bằng n thế năng thì
![]()
Giá trị đại số của tọa độ Z của vật so với mốc bằng:
![]()
Thế năng của vật ở vị trí động năng bằng ba thế năng là
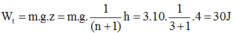


a.
Cơ năng vật:
\(W=W_d+W_t=0,2\cdot 10\cdot180=360\left(J\right)\)
b.
ĐLBT cơ năng với O là điểm tại mặt đất, B là điểm rơi xuống:
\(W_O=W_B\Leftrightarrow\dfrac{1}{2}mv^2=360\)
\(\Leftrightarrow\dfrac{1}{2}\cdot0,2\cdot v^2=360\Leftrightarrow v=60\left(\dfrac{m}{s}\right)\)
ĐLBT cơ năng với O là điểm tại mặt đất, A là điểm động năng bằng thế năng:
\(W_A=W_O\Leftrightarrow2mgh=\dfrac{1}{2}mv^2\)
\(\Leftrightarrow2\cdot0,2\cdot10\cdot h=\dfrac{1}{2}\cdot0,2\cdot60^2\)
\(\Leftrightarrow h=90m\)
c.
ĐLBT cơ năng với O là điểm tại mặt đất, C là điểm động năng bằng 3 lần thế năng:
\(\Leftrightarrow W_O=W_C\Leftrightarrow360=\dfrac{4}{3}mv^2=\dfrac{4}{3}\cdot0,2\cdot v^2\)
\(\Leftrightarrow v\approx36,7\left(\dfrac{m}{s}\right)\)
d.
Độ cao: \(h'=\dfrac{h}{n+1}\)
Vận tốc: \(v'=\sqrt{\dfrac{gh}{\dfrac{1}{2}\left(\dfrac{1}{n}+1\right)}}\)