Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v=v_0+at\)\(=-3t+6\)
\(\Rightarrow v_0=6m\)/s và \(a=-3m\)/s2
Phương trình chuyển động của vật:
\(x=x_0+v_0t+\dfrac{1}{2}at^2=6t+\dfrac{1}{2}\cdot\left(-3\right)\cdot t^2=6t-\dfrac{3}{2}t^2\)

Bài 1:
a, pt chuyển động của vật 1: x=x0+vt => x=20t
pt chuyển động của vật 2: x=x0+ v0t+1/2at^2 => x=1/2*0.4*t^2 => x=0.2t^2
ta có khi 2 vật gặp nhau thì x1=x2=> 20t=0.2.t^2 => t=100s
thay vào pt1 ta được x=2000m
vậy thời gian 2 vật gặp nhau là 100s kể từ khi xuất phát. và cách A là 2000m
b, pt vận tốc vật 2: v=v0+at => v=0.4*t
Gọi độ dài của quãng đường AB là s (km)
Theo báo ra ta có phương trình :
0.5s / 30 + 0.5s /45 =2 (h)
-> s =72 km
Vận tốc của xe thứ 2 là
v = s/t = 72/2 = 36 km/h

Vật đã đi được 4s
\(v=9-2t\Rightarrow\left\{{}\begin{matrix}v_0=9\\a=-2\end{matrix}\right.\)
\(S=v_0t+\dfrac{1}{2}at^2=20m\)

Chọn D.
Vì t = 0 thì v0 = 10m/s > 0, tức là chiều dương của trục tọa độ được chọn cùng chiều với chuyển động của thang máy
Đối chiếu v = (10 – 2t) (m/s) với công thức v = v0 + at suy ra: v 0 = 10 ( m / s ) a = - 2 ( m / s 2 )
Vật dừng lại khi: v = (10 – 2t) = 0 => t = 5s. Từ t = 0 đến t = 5s vật chuyển động chậm dần đều với gia tốc – 2m/s2 và từ t = 5s đến t = 9s vật chuyển động nhanh dần đều với gia tốc 2m/s2.
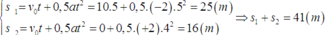


Bạn gõ lộn đề rồi nha
------------
Theo bài ra ta có
v=-2t+10
Lại có , thời điểm ban đầu v=5 (m/s)
=> 5=-2t+10 => t=2,5(s)
5 s tiếp theo , vật có vân tốc là
v' = -2(2,5+5)+10 = -5 (m/s) < 0 (m/s) tức lúc này vật đã dừng lại
vậy khi đó vận tốc của vật là 0 m/s