Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Ta có :
\(x=10+5t-8t^2\)
Có phương trình chuyển động dạng TQ : \(x=x_o+v_ot+\dfrac{1}{2}at^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-4m\backslash s^2\\v_o=5m\backslash s\end{matrix}\right.\)
b/ \(t=1s\)
\(v=v_o+at=5-4.1=1m\backslash s\)
c/ \(v^2-v_o^2=2as\)
\(\Leftrightarrow s=\dfrac{-v_o^2}{2a}=\dfrac{-5^2}{2.\left(-4\right)}=3,125\left(m\right)\)

Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: v = 6 + 4 t (m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình 12.
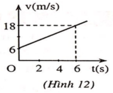
b) Khi v = 18 m/s thì t = 18 − 6 4 = 3 s.
Từ công thức v 2 − v 0 2 = 2 a s
quãng đường s = v 2 − v 0 2 2 a = 18 2 − 6 2 2.4 = 36 m.
c) Phương trình chuyển động: x = 6 t + 2 t 2 (m).
Khi v = 12 m/s thì t = 12 − 6 4 = 1 , 5 s ⇒ tọa độ x = 6.1 , 5 + 2.1 , 5 2 = 13 , 5 m.

a) \(x=10+5t+0,5t^2\)
\(\Rightarrow x_0=10m\); \(v_0=5\)m/s; \(a=1\)m/s2
Đây là chuyển động nhanh dần đều của vật.
b) Xét vật ở thời điểm t=2s:
+ Tọa độ vật: \(x=10+5t+0,5t^2=10+5\cdot2+0,5\cdot2^2=22\left(m\right)\)
+ Vận tốc vật: \(v=v_0+at=5+1\cdot2=7\)(m/s)
+ Quãng đường vật đi: \(S=v_0t+\dfrac{1}{2}at^2=5\cdot2+\dfrac{1}{2}\cdot1\cdot2^2=12\left(m\right)\)

a/ \(x=80t^2+50t+10\)
Phương trình dạng TQ : \(x=x_o+v_ot+\dfrac{1}{2}at^2\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_o=0,5m\backslash s\\a=0,4m\backslash s^2\end{matrix}\right.\)
b/ Tại \(t=1s\)
\(v=v_o+at=0,5+0,4.1=0,9m\backslash s\)
c/ \(v^2-v_o^2=2as\)
\(\Leftrightarrow s=\dfrac{v^2-v_o^2}{2a}=162m\)

\(v=v_0+at\)\(=-3t+6\)
\(\Rightarrow v_0=6m\)/s và \(a=-3m\)/s2
Phương trình chuyển động của vật:
\(x=x_0+v_0t+\dfrac{1}{2}at^2=6t+\dfrac{1}{2}\cdot\left(-3\right)\cdot t^2=6t-\dfrac{3}{2}t^2\)