Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải: Gọi v 13 là vận tốc của người so với mặt nước biển; v 12 là vận tốc của người so với thuyền; v 23 là vận tốc của thuyền so với mặt nước biển.
a. Khi cùng chiều: v 13 = v 12 + v 23 = 1 + 10 = 11 m / s
b. Khi ngược chiều: v 13 = v 23 – v 12 = 10 – 1 = 9 m / s
c. Khi vuông góc: v 13 = v 12 2 + v 23 2 = 10 2 + 1 2 = 10 , 05 m / s

Chọn C
+ Gọi v 13 là vận tốc của người so với mặt nước biển.
v 12 là vận tốc của người so với thuyền
v 23 là vận tốc của thuyền so với mặt nước biển.
+ Khi vuông góc: v 13 = v 12 2 + v 23 2 = 10 2 + 1 2 = 10 , 05 k m / s

Chọn A
+ Gọi v 13 là vận tốc của người so với mặt nước biển.
v 12 là vận tốc của người so với thuyền
v 23 là vận tốc của thuyền so với mặt nước biển.
+ Khi ngược chiều: ![]()

Chọn B
Gọi v 13 là vận tốc của người so với mặt nước biển.
v 12 là vận tốc của người so với thuyền
v 23 là vận tốc của thuyền so với mặt nước biển.
+ Khi cùng chiều: ![]()

Đáp án C
Sau khi hãm tốc :
Quãng đường tàu thứ nhất đã đi được đến khi dừng là
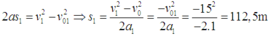
Quãng đường tàu thứ hai đã đi được đến khi dừng là
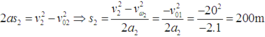
Suy ra, khoảng cách giữa hai tàu là 500 – 112,5 – 200 = 187,5m

(1): người soát vé
(2): đoàn tàu
(3): học sinh.
Chọn chiều dương là chiều chuyển động của đoàn tàu. Ta có: \(\overrightarrow {{v_{13}}} = \overrightarrow {{v_{12}}} + \overrightarrow {{v_{23}}} \)
a) Ta có v12 = 1,5 m/s; v23 = 8 m/s
Người soát vé đi về phía đuôi tàu, người soát vé chuyển động ngược chiều với chiều chuyển động của đoàn tàu nên ta có: \({v_{13}} = - {v_{12}} + {v_{23}} = - 1,5 + 8 = 6,5(m/s)\)
b) Ta có: v12 = 1,5 m/s; v23 = 8 m/s
Người soát vé đi về phía đầu tàu, người soát vé chuyển động cùng chiều với chiều chuyển động của đoàn tàu nên ta có: \({v_{13}} = {v_{12}} + {v_{23}} = 1,5 + 8 = 9,5(m/s)\)
c) Ta có: v12 = 0 m/s; v23 = 8 m/s
=> Vận tốc của người soát vé đối với học sinh là 8 m/s.
