Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
p = 42.k + r. = 2.3.7.k + r
Vì r là hợp số và r < 42 nên r phải là tích của 2 số r = x.y
x và y không thể là 2, 3, 7 và cũng không thể là số chia hết cho 2, 3, 7 được vì nếu thế thì p không là số nguyên tố.
Vậy x và y có thể là các số trong các số {5,11,13, ..}
Nếu x=5 và y=11 thì r = x.y =55>42
Vậy chỉ còn trường hợp x = 5, y = 5. Khi đó r = 25.

Ta có p = 42k+r =2.3.7.k+r( k,r∈N,0<r<42)
Vì p là số nguyên tố nên r không chia hết cho 2, 3,7
Các hợp số nhỏ hơn 42 và không chia hết cho 2 là 9, 15, 21, 25, 27, 33, 35, 39.
Loại đi các số chia hết cho 3, cho 7, chỉ còn 25.
Vậy r = 25.
tk nhé

Toán lớp 6Phân tích thành thừa số nguyên tố
Đinh Tuấn Việt 20/05/2015 lúc 22:51
Theo đề bài ta có:
a = p1m . p2n $\Rightarrow$⇒ a3 = p13m . p23n.
Số ước của a3 là (3m + 1).(3n + 1) = 40 (ước)
$\Rightarrow$⇒ m = 1 ; n = 3 hoặc m = 3 ; n = 1
Số a2 = p12m . p22n có số ước là [(2m + 1) . (2n + 1)] (ước)
-Với m = 1 ; n = 3 thì a2 có (2.1 + 1) . (2.3 + 1) = 3 . 7 = 21 (ước)
-Với m = 3 ; n = 1 thì a2 có (2.3 + 1) . (2.1 + 1) = 7 . 3 = 21 (ước)
Vậy a2 có 21 ước số.
Đúng 4 Yêu Chi Pu đã chọn câu trả lời này.
nguyên 24/05/2015 lúc 16:50
Theo đề bài ta có:
a = p1m . p2n $$
a3 = p13m . p23n.
Số ước của a3 là (3m + 1).(3n + 1) = 40 (ước)
$$
m = 1 ; n = 3 hoặc m = 3 ; n = 1
Số a2 = p12m . p22n có số ước là [(2m + 1) . (2n + 1)] (ước)
-Với m = 1 ; n = 3 thì a2 có (2.1 + 1) . (2.3 + 1) = 3 . 7 = 21 (ước)
-Với m = 3 ; n = 1 thì a2 có (2.3 + 1) . (2.1 + 1) = 7 . 3 = 21 (ước)
Vậy a2 có 21 ước số.
Đúng 0
Captain America

a, Giả sử tồn tại a,b thỏa mãn đề bài
Ta có: \(\frac{1}{a}-\frac{1}{b}=\frac{1}{a-b}\)
\(\Rightarrow\frac{b-a}{ab}=\frac{1}{a-b}\)
\(\Rightarrow\frac{-\left(a-b\right)}{ab}=\frac{1}{a-b}\)
\(\Rightarrow-\left(a-b\right)^2=ab\)
Vì \(\left(a-b\right)^2\ge0\forall a,b\Rightarrow-\left(a-b\right)^2\le0\forall a,b\)
Mà a,b là số nguyên dương => ab > 0
=> Mâu thuẫn
=> Giả sử sai
Vậy không tồn tại a,b thỏa mãn đề
b, https://olm.vn/hoi-dap/question/1231.html


Gọi số nguyên tố cần tìm là x;thương của phép chia là b và dư r.Ta có:
x=42b+r
Ta xét các điều kiện:Đó là số dư khi chia một số chia 42 nên nó nhỏ hơn 42
Do x là số nguyên tố nên r không thể co ước chung là 42,vì nếu có ước chung thì ước đó là ước x =>x không là sô nguyên tố
Ta tìm được số nguyên tố cùng nhau với 42 mà nhỏ hơn 42 và là hợp số là:25
Do x<200 ,số dư 25 nên b <5
Ta có bảng sau:
Với b=0 ,x=42.0+25=25 (L)
Với b=1 ,x=42.1+25=67(N)
Với b=2 ,x=42.2+25=109(N)
Với b=3 ,x=42.3+25=151(N)
Với b=4 ,x=42.4+25=193(N)
Vậy có 4 số thỏa mãn gồm :67;109;151;193.
Chúc Bạn Học Tốt

a) Ta có:
\(p=42k+r=2.3.7.k+r\left(k,r\in N;0< r< 42\right)\)
Vì \(p\) là số nguyên tố nên \(p\) \(⋮̸\) \(2;3;7\)
Các hợp số bé hơn \(42\) và không chia hết cho \(2\) là:
\(9;15;21;25;27;33;35;39\)
Lại đi các số không chia hết cho \(3;7\) ta được \(r=25\)
Vậy \(r=25\)
b) Giải:
Vì \(\overline{ab}^2\) là số chính phương nên \(\left(a+b\right)^3\) là số chính phương
\(\Rightarrow a+b\) là số chính phương.
Đặt \(a+b=x^2\Rightarrow\left(a+b\right)^3=\left(x^2\right)^3=x^6\)
\(\Rightarrow\left\{{}\begin{matrix}x^3< 100\\x^3>8\end{matrix}\right.\)\(\Rightarrow8< x^3< 100\Rightarrow2< x^3< 5\)
\(\Rightarrow\left\{{}\begin{matrix}x=3\\x=4\end{matrix}\right.\) vì \(x\in N\). Xét từng trường hợp ta có:
Nếu \(x=3\Rightarrow3^6=729=27^2=\left(2+7\right)^3\) (chọn)
Nếu \(x=4\Rightarrow4^6=4096=64^2\ne\left(6+4\right)^3\) (loại)
Vậy số tự nhiên cần tìm là \(27\)

Vào đây nhé bạn: Câu hỏi của Công chúa Fine - Toán lớp 7 | Học trực tuyến
Kết luận. Nếu p và 8p-1 là số nguyên tố thì 8p+1 là hợp số.
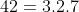 .
.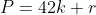 .
.
2. Một số nguyên tố P chia cho 42 có số dư r là hợp số .Tìm r ?
Lời giải. Phân tích
Ta có
Xét
Kết luận. Các số r trên thoả mãn yêu cầu bài toán.