Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot1}{0,5\cdot10^{-3}}=1\cdot10^{-3}m=1mm\)
Tại M trên màn E cách vân trung tâm một khoảng x=3,5mm nên:
\(\Rightarrow x=3,5=k\cdot i=k\cdot1\)
\(\Rightarrow k=3,5\Rightarrow\)Vân tối thứ 4.
Chọn D.

Đáp án C
Khoảng vân: 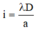
Vị trí của vân sáng bậc 2:
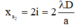
Vị trí của vân tối thứ 3:
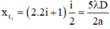
Khoảng cách từ vân sáng bậc 2 đến vân tối thứ 3 nằm về hai phía của vân trung tâm là:
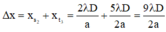

a) Trong khoảng PQ có 11 vân sáng, đồng thời tại P và Q là các vân sáng nên trong khoảng PQ có 10 khoảng vân.
Độ rộng mỗi khoảng vân: \(i=\frac{PQ}{10}=\frac{3}{10}=0,3mm\)
b) Từ công thức \(x_s=\frac{D}{a}k\text{λ}=k.i\). Với \(x_{M1}=0,75mm;i=0,3mm\)
Suy ra \(k=2,5\). Vậy \(M_1\) không thể là vân sáng.
Từ công thức tọa độ vân tối: \(x_1=\frac{D}{a}\left(2k+1\right)\frac{\text{λ}}{2}\Rightarrow k=2\)
Vậy tại \(M_1\)là vân tối.
c) Khoảng cách \(M_1M_2=1,8mm=6i\) tức tại \(M_2\)cũng là vân tối.
Mình góp ý một chút cách làm câu b của bạn Sky SơnTùng
Ta có: i = 0,3mm
\(x_{M1}=0,75mm=2,5i\)
Do vậy, M1 là vân tối thứ ba.
(Vân sáng cách vân trung tâm nguyên lần khoảng vân, vân tối cách vân trung tâm bán nguyên khoảng vân)

Đáp án D
Khoảng vân 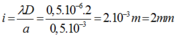
*Khoảng cách giữa một vân sáng và một vân tối cạnh nhau được tính bởi
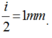 .
.

Chọn B
Ta có: 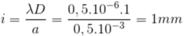
Tại điểm M ta có:
x = 3,5mm = 3,5i => Vân tối thứ 4

Cách giải: Đáp án D
Ta có

Vậy tại M lúc sau phải là vị trí của vân tối của λ2.Từ kết quả trên ta suy ra: MN = 10i1 =14i2 .Vậy trên đoạn MN có 15 vân tối.
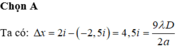

\(i = \frac{\lambda D}{a} = \frac{0,5.1}{0,5} = 1 mm.\)
Số vân sáng trên trường giao thoa L là \(N_S =2 |\frac{L}{2i}|+1 = 2.|\frac{13}{2.1}|+1 = 2.6+1=13\)
Số vân tối trên trường giao thoa L là \(N_t =2 |\frac{L}{2i}+0,5| = 2.|\frac{13}{2.1}+0,5| = 2.7=14.\)
Chú ý: \(|\frac{L}{2i}|\) gọi là lấy phần nguyên của số \(\frac{L}{2i}\).
Ví dụ \(\frac{L}{2i} = 6,5 => |\frac{L}{2i}| = 6.\)
Chọn đáp án.A.