Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật II Niuton ta có:
\(\overrightarrow{F}+\overrightarrow{Fms}+\overrightarrow{N}+\overrightarrow{P}\) = ma
Chiếu lên Oy:N=P=mg
Chiếu lên Ox: -Fms+F=ma
\(\Rightarrow a=\frac{F-Fms}{m}=\frac{F-kmg}{m}\)
Ta có F.\(\Delta\)t=60
F=60/3=20N
\(\Rightarrow\)a=0,15m/s^2
\(\Rightarrow\)v=at=0,15.30=4,5m/s

Áp dụng định luật II Niuton:
\(\overrightarrow{Fms}+\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F}\)= ma
Chiếu lên Oy N=P=mg
Chiếu lên Ox: -Fms+F=ma
-k.m.g+F=ma
\(\Rightarrow a=\frac{F-kmg}{m}\)
Ta có F.\(\Delta\)t=150
⇒⇒F=30N
⇒⇒a=0,2m/s^2
Vận tốc của xe sau khi chuyển động một phút là:
v=at=12m/s
Áp dụng định luật II niuton sau khi người đó không đẩy:
Ta có :-Fms=ma
\(\Rightarrow\)-k.m.g=ma
\(\Rightarrow\)a=-kg=-0,1m/s^2
Áp dụng công thức Vt=v+at
\(\Rightarrow t=\frac{Vt-v}{a}=\frac{0-12}{-0,1}=120s\)
Vậy vận tốc của xe sau khi c/đ 1 phút là 6m/s
Xe sẽ dừng lại sau 120s

Định luật ll Niu tơn: \(\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
\(\Rightarrow F-F_{ms}=m.a\)
\(\Rightarrow F-\mu mg=m.a\)
Gia tốc thùng:
\(\Rightarrow a=\dfrac{F-\mu mg}{m}=\dfrac{180-0,25\cdot50\cdot9,8}{50}=1,15\left(m/s^2\right)\)

Theo định luật II Newton: \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}+\overrightarrow{F_{ms}}=m.\overrightarrow{a}\)
Chiếu phương trình lên Oy: \(N-P=0\Rightarrow N=P=mg=40.9,8=392\left(N\right)\)
Chiếu phương trình lên Ox: \(-F_{ms}+F=ma\)
\(\Rightarrow-\mu N+F=ma\)
\(\Rightarrow a=\dfrac{F-\mu N}{m}=\dfrac{240-0,25.392}{40}=3,55\left(\dfrac{m}{s^2}\right)\)
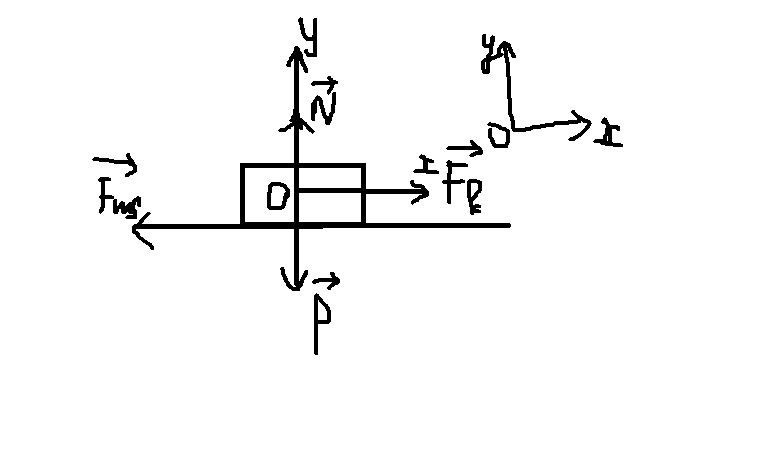
Chọn hệ trục Oxy như hình.
Chiều dương là chiều chuuyeern động.
Theo định luật ll Niu-tơn:
\(\overrightarrow{Fms}+\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F}=m.\overrightarrow{a}\) (1)
Chiếu lên trục Ox ta đc:
\(F-F_{ms}=ma\) (2)
Chiếu (1) lên trục Oy ta đc:
\(N-P=0\Rightarrow N=P=mg\) (3)
\(F_{ms}=\mu\cdot N\) (4)
Từ \(\left(2\right).\left(3\right),\left(4\right)\) ta suy ra:
\(F-F_{ms}=ma\)
\(\Rightarrow a=\dfrac{F-F_{ms}}{m}=\dfrac{240-0,25\cdot40\cdot9,8}{40}=3,55\)m/s2

200g=0,2kg
các lực tác dụng lên vật khi ở trên mặt phẳng nghiêng
\(\overrightarrow{P}+\overrightarrow{N}=m.\overrightarrow{a}\)
chiếu lên trục Ox có phương song song với mặt phẳng nghiêng, chiều dương cùng chiều chuyển động
P.sin\(\alpha\)=m.a\(\Rightarrow\)a=5m/s2
vận tốc vật khi xuống tới chân dốc
v2-v02=2as\(\Rightarrow\)v=\(4\sqrt{5}\)m/s
khi xuống chân dốc trượt trên mặt phẳng ngang xuất hiện ma sát
các lực tác dụng lên vật lúc này
\(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}=m.\overrightarrow{a'}\)
chiếu lên trục Ox có phương nằm ngang chiều dương cùng chiều chuyển động của vật
-Fms=m.a'\(\Rightarrow-\mu.N=m.a'\) (1)
chiếu lên trục Oy có phương thẳng đứng chiều dương hướng lên trên
N=P=m.g (2)
từ (1),(2)\(\Rightarrow\)a'=-2m/s2
thời gian vật chuyển động trên mặt phẳng đến khi dừng lại là (v1=0)
t=\(\dfrac{v_1-v}{a'}\)=\(2\sqrt{5}s\)

Chọn chiều của lực tác dụng làm chiều dương:
F m s = μ t mg = 0,35.55.9,8 = 188,65 N ≈ 189 N
Do đó a = (F - F m s )/m = (220 - 189)/55 ≈ 0,56(m/ s 2 )
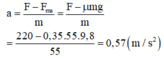
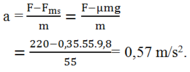
lực đẩy:
\(F=\dfrac{\Delta p}{t}\)=20N
theo định luật II niu tơn
\(\overrightarrow{F}+\overrightarrow{F_{ms}}+\overrightarrow{N}+\overrightarrow{P}=m.\overrightarrow{a}\)
chiếu lên trục Ox phương nằm ngang, chiều dương cùng chiều chuyển động
\(F-F_{ms}=m.a\)
\(\Rightarrow a=\)0,15m/s2
vận tốc sau 15s
v=a.t=2,25m/s
(xung lượng là:\(F.\Delta t\)
mà \(F.\Delta t=\Delta p\)
còn trừ Fms là do lực ma sát ngược chiều dương nên lúc bỏ dấu vectơ là trừ, chiều dương ở đây là trục Ox ở trên nãy chọn...)
Nhưng sao theo sách nó bảo xung lượng bằng tổng các lực tác dụng lên vật trong thời gian đó hay chỉ khi tính theo độ biến thiên