Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(x\) là khoảng cách từ thuyền đến đỉnh tháp (m)
Áp dụng định lý Pythagore ta có:
\({x^2} = {180^2} + {25^2}\)
\({x^2} = 33025\)
\(x = \sqrt {33025} \approx 181,73\) (m)
Vậy khoảng cách từ thuyền đến đỉnh tháp hải đăng là: 181,73m

Gọi chiều cao của tòa tháp là h \(\left(m,h>0\right)\)
Chiều cao của tòa tháp là:
\(\frac{13,1}{0,1}=\frac{h}{2}\Rightarrow h=\frac{13,1\times2}{0,1}=262\left(m\right)\)(TM)
Vậy chiều cao của toà tháp là \(262m\)

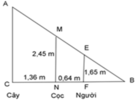
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.
Xét ΔBFE và ΔBNM ta có:
B chung
B E F ^ = B M N ^ (vì EF // MN, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBNM (g - g)
⇒ B F B N = F E N M ⇔ B F B F + F N = F E N M ⇔ B F B F + 0 , 64 = 1 , 65 2 , 45
⇔ 1,65(BF + 0,64) = 2,45.BF
⇔ BF = 1,32m
Xét ΔBFE và ΔBCA có:
B chung
B E F ^ = B A C ^ (vì EF // AC, cặp góc đồng vị bằng nhau)
=> ΔBFE ~ ΔBCA (g - g)
⇒ B F B C = F E C A ⇔ B F B F + F N + N C = F E C A ⇔ 1 , 32 1 , 32 + 0 , 64 + 1 , 36 = 1 , 65 C A
=> CA = 4,15m
Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15m.
Đáp án: D
