Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chân hải đăng là A thì ta để ý thấy. Lần đầu quan sát thì tam giác DAB là nửa tam giác đều
\(\Rightarrow DA^2+AB^2=DB^2\)
\(\Leftrightarrow DA^2+AB^2=4AB^2\)
\(\Leftrightarrow DA^2=3AB^2=3.75^2=11250\)
\(\Leftrightarrow DA=106,066\)
Lần thứ 2 quan sát thì tam giác CAB là tam giác vuông cân
\(\Rightarrow CA=AB=75\)
Vậy quãng đường thuyền đi được là:
\(DC=DA-CA=106,066-75=31,066\)

B: Là vị trí thuyền hiện tại
D: là vị trí thuyền sau 10 phút
AC: chiều cao ngọn hải đăng = 63 m
Xét tg vuông ABC
\(\tan\widehat{ABC}=\tan19^o=\frac{AC}{AB}=\frac{63}{AB}\Rightarrow AB=\frac{63}{\tan19^o}\)
Xét tg vuông ACD có
\(\tan\widehat{ADC}=\tan54^o=\frac{AC}{AD}=\frac{63}{AD}\Rightarrow AD=\frac{63}{\tan54^o}\)
Quãng đường thuyền đi được sau 10' là
\(BD=AB-AD=\frac{63}{\tan19^o}-\frac{63}{\tan54^o}\)

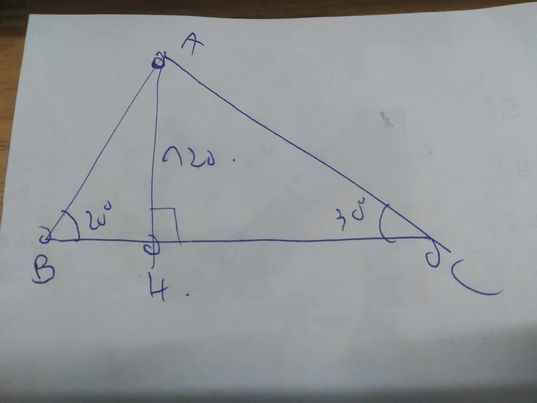
Gọi AH là độ cao của ngọn hải đăng, BC là độ dài quãng đường con thuyền đi được giữa hai lần quan sát.
Theo đề, ta có: AH=120m; \(\widehat{B}=20^0;\widehat{C}=30^0\)
Xét ΔAHB vuông tại H có \(tanB=\dfrac{AH}{HB}\)
=>\(HB=\dfrac{120}{tan20}\simeq329,7\left(m\right)\)
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)
=>\(\dfrac{120}{HC}=tan30\)
=>\(HC=\dfrac{120}{tan30}\simeq207,85\left(m\right)\)
BC=BH+CH=329,7+207,85=537,55(m)
Vậy: Con thuyền đã được 537,55m giữa hai lần quan sát