Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số ghế băng lúc đầu là x ( ghế băng), ( x∈N*, x> 2)
Số học sinh ngồi trên mỗi ghế là 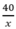 ( học sinh ) .
( học sinh ) .
Khi bớt đi 2 ghế băng thì còn lại x- 2 ( ghế băng ) và khi đó, mỗi ghế có 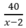 học sinh ngồi.
học sinh ngồi.
Theo giả thiết, nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh nên ta có phương trình:
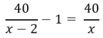
⇔ 40 x − x ( x − 2 ) = 40 ( x − 2 ) ⇔ 40 x − x 2 + 2 x = 40 x − 80 ⇔ − x 2 + 2 x + 80 = 0
Có a = -1, b= 2; c = 80 và ∆ = 2 2 – 4 . ( - 1 ) . 80 = 324
Nên phương trình trên có 2 nghiệm là: x1 = -8 ( loại) và x2 =10 ( thỏa mãn)
Vậy lúc đầu có 10 ghế băng.

Gọi số ghế băng lúc đầu là x ( ghế băng), ( x∈N*, x> 2)
Số học sinh ngồi trên mỗi ghế là 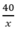 ( học sinh ) .
( học sinh ) .
Khi bớt đi 2 ghế băng thì còn lại x- 2 ( ghế băng ) và khi đó, mỗi ghế có 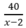 học sinh ngồi.
học sinh ngồi.
Theo giả thiết, nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh nên ta có phương trình:

⇔ 40 x − x ( x − 2 ) = 40 ( x − 2 ) ⇔ 40 x − x 2 + 2 x = 40 x − 80 ⇔ − x 2 + 2 x + 80 = 0
Có a = -1, b= 2; c = 80 và ∆ = 2 2 – 4 . ( - 1 ) . 80 = 324
Nên phương trình trên có 2 nghiệm là: x1 = -8 ( loại) và x2 =10 ( thỏa mãn)
Vậy lúc đầu có 10 ghế băng.

Gọi số ghế băng ban đầu là x(ghế)(x thuộc N*).
số học sinh/ghế là 40/x(học sinh).
số ghế khi bớt đi là : x-2(ghế)
số học sinh/ghế khi bớt ghế là : 40/x-2 (học sinh)
Do khi bớt đi 2 ghế ,số học sinh phải thêm 1 vào mỗi hàng nên ta có pt sau:
40/x-2 - 40/x = 1
<=>40x/x(x-2) - 40(x-2 ) /x(x-2) = x(x-2)/x(x-2)
==>40x - 40 (x-2) =x(x-2)
<=> 40x - 40x + 80 = x2 - 2x
<=> x2 - 2x - 80 = 0
Giải đenta ' ta có: đenta ' = (-1)2 - 1(-80)=1 + 80 = 81>0
==>Phương trình có hai nghiệm phân biệt
x1 =(-b' + 9)/a=(1 + 9 )/1=10.(thỏa mãn)
x2 =(-b' - 9)/a =( 1 - 9)/1 = -8(loại).
Vậy số ghế băng ban đầu là 10 ghế.

Gọi số dãy ghế lúc ban đầu là x(dãy)
(Điều kiện: \(x\in Z^+\))
Số người ngồi trên 1 dãy ghế ban đầu là \(\dfrac{80}{x}\left(người\right)\)
Số dãy ghế khi bớt đi 2 dãy là x-2(dãy)
Số người ngồi trên 1 dãy ghế khi bớt đi 2 dãy ghế là \(\dfrac{80}{x-2}\left(người\right)\)
Theo đề, ta có phương trình:
\(\dfrac{80}{x-2}-\dfrac{80}{x}=2\)
=>\(\dfrac{80x-80\left(x-2\right)}{x\left(x-2\right)}=2\)
=>\(\dfrac{160}{x\left(x-2\right)}=2\)
=>x(x-2)=80
=>\(x^2-2x-80=0\)
=>(x-10)(x+8)=0
=>\(\left[{}\begin{matrix}x-10=0\\x+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=10\left(nhận\right)\\x=-8\left(loại\right)\end{matrix}\right.\)
Vậy: Số dãy ghế ban đầu là 10 dãy
Số người ngồi trên 1 dãy ban đầu là 80:10=8 người

Gọi số chỗ ngồi ban đầu ở mỗi dãy là x
Theo đề, ta có: 80/x+2=80/x-2
=>80/(x+2)-80/x=-2
=>\(\dfrac{80x-80x-160}{x\left(x+2\right)}=-2\)
=>x^2+2x-80=0
=>x=8


Phan Minh Anh
Gọi x là số ghế băng ban đầu (x thuôc N*)
Suy ra số học sinh ở mỗi ghế băng là 40:x
Nếu bớt đi 2 ghế băng (x-2) thì mỗi ghế còn lại phải xếp thêm 1 hs (x+1)
Hay (x-2).(x+1) =40
<=> x2 -2x -80 =0
<=> x=10
Vậy số ghế băng ban đầu là 10 ghế