Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Áp dụng hệ thức vuông pha giữa u L và u R u 2 R U 2 Ỏ R + u 2 L U 2 0 L = 1
Cách giải:
Từ biểu thức 625u2R + 256 u2L = 1600 ta có:
625 u 2 R 1600 + 256 u 2 L 1600 = 1 ⇒ u 2 R 40 25 2 + u 2 L 40 16 2 = 1 ⇒ U 0 R = 40 25 = 1 , 6 V ; U 0 L = 40 16 = 2 , 5 V ⇒ I 0 = U 0 R 32 = 0 , 05 A Z L = U 0 L I 0 = 50 Ω ⇒ L = Z L ω = 1 2 π ( H )

Bài 1:
Trước hết có \(Z_L=Z_C=100\Omega\Rightarrow Z_m=100\sqrt{3}\Omega\Rightarrow I=\sqrt{\frac{7}{3}}A\)
suy ra \(U_{AN}=U_{BM}=200\sqrt{\frac{7}{3}}V\) ( sao số xấu thế?)
Vẽ giản đồ vecto dễ thấy $U_{AN}$ chậm pha hơn $U_{BM}$ một góc \(\frac{\pi}{3}\)
\(u_{AN}=200\sqrt{\frac{14}{3}}\cos\left(100\pi t+\varphi\right)=100\sqrt{3}\) \(\Rightarrow u_{BM}=200\sqrt{\frac{14}{3}}\cos\left(100\pi t+\varphi+\frac{\pi}{3}\right)\)
Mặt khác $U_{AN}$ đang tăng nên \(\sin\left(100\pi t+\varphi\right)< 0\) Từ đó áp dụng công thức khai triển $\cos$ suy ra \(u_{BM}=50\sqrt{3}+200\sqrt{\frac{989}{336}}\) (V)
Bài 2: Nối tắt 2 đầu điện trở?

Đáp án A
+ Câu A: vì u L và u R vuông pha nên:
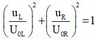
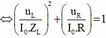
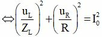 => A sai.
=> A sai.
+ Câu B ![]() => Đúng
=> Đúng
+ Câu C hiển nhiên đúng.
+ Câu D: vì
u
L
và i vuông pha nên: 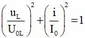

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

\(Z_L=60\Omega\)
\(Z_C=100\Omega\)
Công suất tỏa nhiệt trên R là:
\(P=I^2R=\frac{U^2}{R^2+\left(Z_L-Z_C\right)^2}.R\)
\(\Rightarrow80=\frac{80^2.R}{R^2+\left(60-100\right)^2}\)
\(\Rightarrow R^2-80R+40^2=0\)
\(\Rightarrow R=40\Omega\)
Chọn C
\(\leftrightarrow\frac{u^2_R}{\left(\frac{8}{5}\right)^2}+\frac{u^2_L}{\left(\frac{5}{2}\right)^2}=1\)
Điều kiện :
\(\begin{cases}u_R\le\frac{8}{5}\left(V\right)\\u_L\le\frac{5}{2}\left(V\right)\end{cases}\)
\(\Rightarrow U_{\text{oR}}=\frac{8}{5}\left(V\right);U_{0L}=\frac{5}{2}\left(V\right)\)
\(\Rightarrow\frac{R}{\omega L}=\frac{8}{5}.\frac{2}{5}=\frac{16}{25}\leftrightarrow L=\frac{25R}{16L}=\frac{1}{2\pi}\left(H\right)\)
Đáp án C