Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi L = L 1 thì dòng điện cùng pha với điện áp → hiện tượng cộng hưởng → Z C = Z L 1 = 2 π f L 1 .
Khi L = L 2 xảy ra cực đại điện áp hiệu dụng trên cuộn dây Z L 2 = R 2 + Z C 2 Z C ⇔ 2 π f L 2 = 50 2 + 2 π f L 1 2 2 π f L 1 → f = 25 Hz.
Đáp án A

Chọn B
U RL = | · Z RL = U R 2 + Z L 2 R 2 + Z L - Z C 2 ∉ R ⇔ Z L 2 = Z L - Z C 2 ⇒ Z C = 2 Z L Z = R 2 + Z L 2 = U I = 100 Ω ⇒ Z L ≤ 100 Ω ⇒ Z C = 2 Z L ≤ 200 Ω ⇒ C ≥ 1 100 π 200 = 50 π 10 - 6 F

Giải thích: Đáp án C
Lúc đầu chưa mắc C, mạch chỉ có RL: 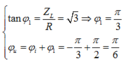
*Khi mắc thêm C:
![]() => Mạch xảy ra hiện tượng cộng hưởng.
=> Mạch xảy ra hiện tượng cộng hưởng.
![]()

Chọn B
f = f1. → Zd = R 2 + Z L 1 2 =100Ω => R 2 + Z L 1 2 = 10 4
Khi UC = UCmax thì ZC1 = R 2 + Z L 1 2 Z L 1 => L C = R 2 + Z L 1 2 = 10 4 (*)
Khi f = f2; I = Imax trong mạch có cộng hưởng điện => ZC2 = ZL2
LC = 1 ω 2 2 = 1 4 π 2 f 2 2 (**)
Từ (*) và (**) => L2 = 10 4 4 π 2 f 2 2 => L = 10 2 2 πf 2 = 1 2 π = 0 , 5 π H

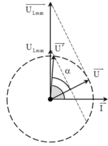
Biểu diễn vecto chung gốc I cho các điện áp.
→ Từ hình vẽ, ta có cosα = 0,5 → α=π/3.
Mặc khác φ = α + 0,25φ → φ = 1,4 rad.
Đáp án C

Chọn C
Gọi điện trở của đoạn mạch X là R:
cos φ = U r + U R U = cos 30 0 = 3 2
Ur + UR = 3 2 U = 60 3 V và Ur = I.r = 30 3 => UR = 60 3 – Ur = 30 3 V
UR=Ur => R = r = 100 3
Công suất tiêu thụ trên mạch X là : PX = PR =I2R=9 3 W

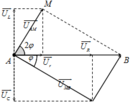
Biễu diễn vecto các điện áp. Mạch xảy ra cộng hưởng → U → cùng phương, chiều với vecto I → . Từ hình vẽ ta có:
U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ
Mặc khác, áp dụng định lý sin trong tam giác AMB:
U sin 180 − 3 φ = U A M sin φ → sin 3 φ − 5 4 sin φ = 0
→ 4 sin 3 φ − 7 4 sin φ = 0
Phương trình cho ta nghiệm sin φ = 7 4 → φ ≈ 41 0 .
→ U M B = U A M 2 + U 2 − 2 U A M U M B cos 2 φ ≈ 240 V
Đáp án D

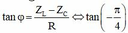
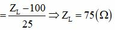
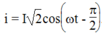 i = I
i = I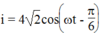
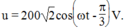
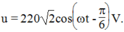
Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)