Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi kích thước chiều dài và chiều rộng ban đầu lần lượt là x;y (m) (x>y>3)
Diện tích mảnh đất ban đầu là: 80m2, ta có pt: xy=80 (1)
Chiều dài mảnh đất sau khi tăng 10m là: x+10 (m)
Chiều rộng mảnh đất sau khi giảm 3m là: y-3 (m)
Diện tích mới của mảnh đất là: (x+10)(y-3) (m2)
Do diện tích mới tăng thêm 20m2 nên diện tích mới khi đó là: 80+20=100 (m2)
Ta có pt:\(\left(x+10\right)\left(y-3\right)=100\) (2)
Từ (1) (2) ta có hệ: \(\left\{{}\begin{matrix}xy=80\\\left(x+10\right)\left(y-3\right)=100\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\xy-3x+10y-30=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\-3x+10y=50\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xy=80\\y=\dfrac{50+3x}{10}\end{matrix}\right.\)
\(\Rightarrow x\left(\dfrac{50+3x}{10}\right)=80\)
\(\Leftrightarrow3x^2+50x-800=0\Leftrightarrow\left(x-10\right)\left(2x+80\right)=0\)
\(\Leftrightarrow x=10\) (do 2x+80>0 với mọi x>3)
\(\Rightarrow y=8\) (tm)
Vậy kích thước chiều dài và chiều rộng ban đầu là 10m và 8m

- Gọi chiều dài và chiều rộng của hình chữ nhật đó lần lượt là x, y ( x > y > 0 , m )
- Diện tích ban đầu của hình chữ nhật đó là : xy ( m2 )
- Theo dữ kiện bài ra ta có hệ phương trình :
\(\left\{{}\begin{matrix}\left(x+2\right)\left(y+2\right)=xy+66\\\left(x-2\right)\left(y-3\right)=xy-74\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy+2x+2y+4=xy+66\\xy-3x-2y+6=xy-74\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=62\\-3x-2y=-80\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=18\\y=13\end{matrix}\right.\) ( TM )
Vậy ...

Gọi x(m) là chiều rộng của hcn ⇒ 4x (m) là chiều dài của hcn.
Theo đề: \((x-2).(2.4x)=x.4x+20\Leftrightarrow x^2-4x-5=0\Leftrightarrow\left[\begin{array}{} x=5\\ x=-1(loại) \end{array} \right.\)
Vậy mảnh đất hcn có chiều rộng là 5m, chiều dài là 4.5=20m

- gọi cdai và crong lần lượt là x, y (m) (x,y >0)
- theo bài ra ta có hệ pt: (x+2)(y+2)=xy+66
(x-2)(y-3)=xy-74
=> x=... , y=...
Vậy....

Gọi chiều rộng của mảnh đất là x (m, x > 0).
Diện tích bằng 240 m2 ⇒ Chiều dài mảnh đất là: 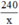 (m).
(m).
Diện tích mảnh đất sau khi tăng chiều rộng 3m, giảm chiều dài 4m là:
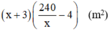
Theo bài ra: diện tích mảnh đất không đổi nên ta có phương trình:
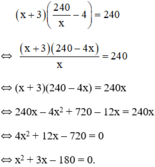
Có a = 1; b = 3; c = -180 ⇒ Δ = 32 – 4.1.(-180) = 729
Phương trình có hai nghiệm:
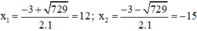
Trong hai nghiệm chỉ có nghiệm x = 12 thỏa mãn điều kiện.
Vậy mảnh đất có chiều rộng bằng 12m, chiều dài bằng 240 : 12 = 20 (m).

Nửa chu vi mảnh đất: \(25-x\) (m)
Gọi chiều rộng mảnh đất là x (m) với 0<x<50
Chiều dài mảnh đất là: \(25-x\) (m)
Chiều dài khi tăng 2 lần: \(2\left(25-x\right)\)
Chiều rộng khi giảm 5m: \(x-5\)
Nửa chu vi mới của mảnh đất là: \(2\left(25-x\right)+x-5=45-x\)
Do chu vi mảnh đất tăng 20m nên ta có pt:
\(2\left(45-x\right)=50+20\)
\(\Rightarrow x=10\left(m\right)\)
Chiều dài mảnh đất là: \(25-10=15\left(m\right)\)
Diện tích: \(15.10=150\left(m^2\right)\)