Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
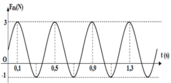
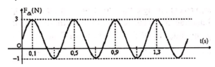
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
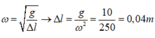
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 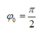 rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm

Đáp án D
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
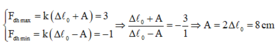
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
![]()
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
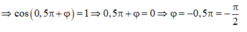
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )

Chọn C
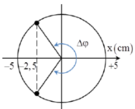
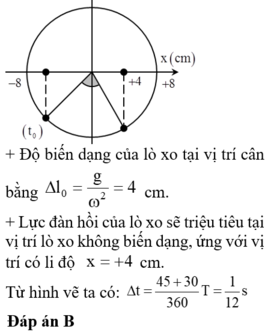
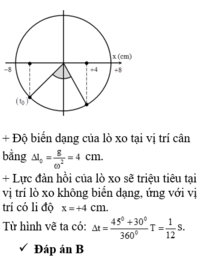
+ Độ biến dạng của lò xo tại vị trí cân bằng:
![]()
+ Lực đàn hồi tác dụng lên vật thỏa mãn:
|Fđh| > 1,5N khi |Δl| > 0,015m = 1,5cm hay -2,5 cm < x < 5cm.
+ Từ hình vẽ ta xác định được khoảng thời gian tương ứng là:
![]()

Chọn C
Phương pháp: Sử dụng đường tròn lượng giác
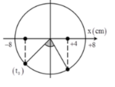
Cách giải: Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s. Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác
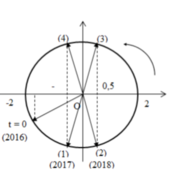
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N. Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
→ Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
t = 504 T + T 2 π . π 3 + π 2 - a r c cos 0 , 5 4 = 201 , 67 s

\(ptlđ:x=6cos\left(5\pi t\right)\Rightarrow\omega=5\pi\left(rad/s\right)\) ( Không quan trọng cái chỗ cộng bao nhiêu nha! Chỉ quan tâm đến trước chữ t)
Mặt khác: \(\omega=\sqrt{\dfrac{k}{m}}\Rightarrow k=m\omega^2=1.\left(5\pi\right)^2=25\pi^2=250\left(N/m\right)\)
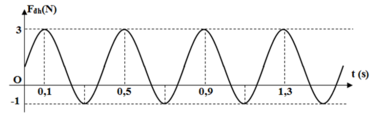


Chọn A
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.