Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Sử dụng đường tròn lượng giác
Cách giải:
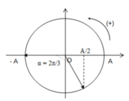
Biểu diễn bằng hình vẽ ta được thời gian ngắn nhất vật đi từ vị trí x1 = - A đến x2 = A/2 tương ứng với góc quét α = 2π/3 => Thời gian t = α/ω = T/3 = 1s => T = 3s.

Theo bài ra ta có tần số góc ω = 2 π /T = 10 π (rad/s)
Tại thời điểm ban đầu vật ở vị trí cân bằng và đi theo chiều âm nên ta có
![]()
Phương trình dao động của vật là: x = 0,2cos(10 π t + π /2)

Để tìm tần số dao động của con lắc, ta có công thức:
f = 1/T
Trong đó: f là tần số dao động (Hz) T là chu kì dao động (s)
Theo đề bài, khoảng thời gian để vật nhỏ của con lắc có độ lớn gia tốc không vượt quá 100 cm/s là T/3. Độ lớn gia tốc của con lắc được tính bằng công thức:
a = -ω²x
Trong đó: a là gia tốc (cm/s²) ω là góc tốc độ góc của con lắc (rad/s) x là biên độ dao động (cm)
Ta có thể tính được ω bằng công thức:
ω = 2πf
Thay vào công thức gia tốc, ta có:
a = -(2πf)²x = -4π²f²x
Đề bài cho biết gia tốc không vượt quá 100 cm/s, nên ta có:
100 ≥ 4π²f²x
Với x = 5 cm, ta có:
100 ≥ 4π²f²(5)
Simplifying the equation:
5 ≥ π²f²
Từ đó ta có:
f² ≤ 5/π²
f ≤ √(5/π²)
f ≤ √(5/π²) ≈ 0.798 Hz
Vậy tần số dao động của con lắc là khoảng 0.798 Hz.

Khoảng thời gian ngắn nhất để vật đi từ vị trí cân bằng đến vị trí biên là ∆ t = 0 , 25 T = 1 s
Đáp án B

Đáp án C
Ta có : tại thời điểm x = -10 cm vật ở vị trí trên đường tròn số 2 hoặc số 3
Giả sử ta chọn nó đang ở vị trí trên đường tròn số 2 , xét tiếp sau đó khoảng thời gian 3 T 4 ở vị trí đường tròn số 1.
Mà vận tốc v nhanh pha hơn li độ x một góc là π 2
x 1 v à v và v cùng pha ta có : - 10 A = - 100 ω A ⇒ ω = 10 r a d / s


