Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp:
Tính thể tích mỗi viên bi hình cầu: V = 4 3 π R 3 ⇒ 5 viên có thể tích
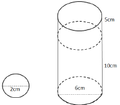
Tính thể tích lượng nước ban đầu (cột nước hình trụ): V 2 = V n = π R 2 h .
Tính tổng thể tích cả bi và nước lúc sau V = V 1 + V 2 , từ đó suy ra chiều cao cột nước lúc sau và khoảng cách từ mặt nước đến miệng cốc.
Cách giải:
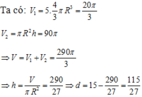
Chú ý khi giải:
Các em có thể sẽ quên không tính thể tích của 5 viên bi, hoặc nhầm lẫn đường kính 6cm thành bán kinh 6cm dẫn đến các thể tích bị sai.
Đáp án C
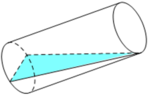
Chọn hệ trục như hình vẽ và cắt mặt nước theo thiết diện là tam giác vuông PNM. Hình chiếu vuông góc của mặt phẳng thiết diện xuống đáy là nửa đường tròn đường kính AB
Ta có:
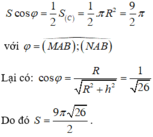
Cách giải:
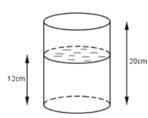
Để uống được nước thì con quạ phải thả các viên bi vào cốc sao cho mực nước trong cốc dâng lên ít nhất: 20 -12 - 6 = 2( cm)
Khi đó, thể tích của mực nước dâng lên là
Đáp án D
Phương pháp:
+) Thể tích khối nước ít nhất cần dâng lên = Tổng thể tích đá thả vào.
+) Số viên đá = Tổng thể tích đá thả vào : Thể tích 1 viên đá
Đáp án C
Chuẩn hóa bán kính của viên bi là 1 => Chiều cao của cốc là h = 2.
+) Thể tích của viên bi là V 1 = 4 π 3 . Gọi R, r lần lượt là bán kính của miệng cốc và đáy cốc.
+) Thể tích của cốc ( khối nón cụt ) là V 2 = πh 3 R 2 + R r + r 2 = 2 π 3 R 2 + R r + r 2
+) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
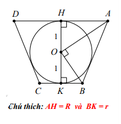
+) Xét mặt cắt của cốc khi thả viên bi vào trong cốc ( hình vẽ bên)
Dễ thấy ABCD là hình thang cân ⇒ O A 2 + O B 2 = A B 2 ( 2 )
Mà O A 2 = R 2 + 1 O B 2 = r 2 + 1 và A B 2 = A H - B K 2 + H K 2 = R - r 2 + 4 ( 3 )
Từ (2) và (3) ⇒ R 2 + r 2 + 2 = R - r 2 + 4 ⇔ R r = 1 ( 4 )
Từ (1) và (4) ⇒ R 2 + R r + r 2 = 4 R r ⇔ R r 2 = 3 R r + 1 = 0
⇔ R r = 3 + 5 2 . Vậy tỉ số cần tính là 3 + 5 2
Đáp án C.
Ta có
V b i = V m c = 4 3 h 2 3 . π ; V c o c = V n c = π 3 . h . R 2 + r 2 + R r
Mà V n c = 2 V m c do vậy π 3 h R 2 + r 2 + R r = 2. 4 3 . h 2 3 π
⇔ R 2 + r 2 + R . r = h 2
Mà ⇔ R 2 + r 2 + R . r = h 2 do vậy
P T ⇔ r R 2 − 3 r R + 1 = 0 ⇔ r R = 3 + 5 2 t m r R = 3 − 5 2 l
Vậy ta chọn C.
Đáp án D
Tổng thể tích nước và 5 viên bi là: 120 + 5. 4 π .1 3 3 ≈ 140 , 94 m l
Lượng nước trong cốc có dạng hình trụ, với bán kính là: 6 − 0 , 2.2 2 = 2 , 8 c m
Khi đó, chiều cao h' của mực nước tinh từ đáy trong của cốc được tính từ:
π .2 , 8 2 h ' = 140 , 94 ⇔ h ' = 5 , 72
Chiều cao từ đáy trong côc đến mép cốc là: 9 − 1 = 8
Vậy mặt nước trong cách mép: 8 − 5.72 = 2 , 28.