Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Tổng thể tích nước và 5 viên bi là: 120 + 5. 4 π .1 3 3 ≈ 140 , 94 m l
Lượng nước trong cốc có dạng hình trụ, với bán kính là: 6 − 0 , 2.2 2 = 2 , 8 c m
Khi đó, chiều cao h' của mực nước tinh từ đáy trong của cốc được tính từ:
π .2 , 8 2 h ' = 140 , 94 ⇔ h ' = 5 , 72
Chiều cao từ đáy trong côc đến mép cốc là: 9 − 1 = 8
Vậy mặt nước trong cách mép: 8 − 5.72 = 2 , 28.
Đáp án B
Phương pháp:
Tính thể tích mỗi viên bi hình cầu: V = 4 3 π R 3 ⇒ 5 viên có thể tích
Tính thể tích lượng nước ban đầu (cột nước hình trụ): V 2 = V n = π R 2 h .
Tính tổng thể tích cả bi và nước lúc sau V = V 1 + V 2 , từ đó suy ra chiều cao cột nước lúc sau và khoảng cách từ mặt nước đến miệng cốc.
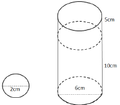
Cách giải:
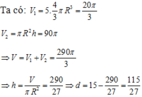
Chú ý khi giải:
Các em có thể sẽ quên không tính thể tích của 5 viên bi, hoặc nhầm lẫn đường kính 6cm thành bán kinh 6cm dẫn đến các thể tích bị sai.
Cách giải:
Để uống được nước thì con quạ phải thả các viên bi vào cốc sao cho mực nước trong cốc dâng lên ít nhất: 20 -12 - 6 = 2( cm)
Khi đó, thể tích của mực nước dâng lên là
Đáp án D
Phương pháp:
+) Thể tích khối nước ít nhất cần dâng lên = Tổng thể tích đá thả vào.
+) Số viên đá = Tổng thể tích đá thả vào : Thể tích 1 viên đá
Đáp án C
Chuẩn hóa bán kính của viên bi là 1 => Chiều cao của cốc là h = 2.
+) Thể tích của viên bi là V 1 = 4 π 3 . Gọi R, r lần lượt là bán kính của miệng cốc và đáy cốc.
+) Thể tích của cốc ( khối nón cụt ) là V 2 = πh 3 R 2 + R r + r 2 = 2 π 3 R 2 + R r + r 2
+) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
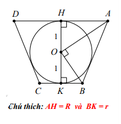
+) Xét mặt cắt của cốc khi thả viên bi vào trong cốc ( hình vẽ bên)
Dễ thấy ABCD là hình thang cân ⇒ O A 2 + O B 2 = A B 2 ( 2 )
Mà O A 2 = R 2 + 1 O B 2 = r 2 + 1 và A B 2 = A H - B K 2 + H K 2 = R - r 2 + 4 ( 3 )
Từ (2) và (3) ⇒ R 2 + r 2 + 2 = R - r 2 + 4 ⇔ R r = 1 ( 4 )
Từ (1) và (4) ⇒ R 2 + R r + r 2 = 4 R r ⇔ R r 2 = 3 R r + 1 = 0
⇔ R r = 3 + 5 2 . Vậy tỉ số cần tính là 3 + 5 2
Đáp án C.
Ta có
V b i = V m c = 4 3 h 2 3 . π ; V c o c = V n c = π 3 . h . R 2 + r 2 + R r
Mà V n c = 2 V m c do vậy π 3 h R 2 + r 2 + R r = 2. 4 3 . h 2 3 π
⇔ R 2 + r 2 + R . r = h 2
Mà ⇔ R 2 + r 2 + R . r = h 2 do vậy
P T ⇔ r R 2 − 3 r R + 1 = 0 ⇔ r R = 3 + 5 2 t m r R = 3 − 5 2 l
Vậy ta chọn C.
