Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Nếu tia khúc xạ truyền gần sát mặt phân cách hai môi trường trong suốt thì góc tới bằng góc phản xạ toàn phần

+ Áp dụng định luật khúc xạ cho môi trường tới 1 và môi trường khúc xạ 2:


Đáp án: C
Ta có:
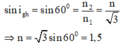
Để góc tới i ≥ 60o luôn có phản xạ toàn phần thì n ≤ 1,5.

3/ \(n\sin i=\sin60^0;\) \(i=90-r\Rightarrow i=30^0\)
\(\Rightarrow n=\dfrac{\sin60^0}{\sin30^0}=\sqrt{3}\)
5/ \(D=\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow2=\dfrac{1}{0,25}+\dfrac{1}{d'}\Rightarrow d'=-50\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{50}{25}=2\)
=>D. Anh ao, cach thau kinh 50cm, k=2
7/ \(d=\dfrac{d'f}{d'-f}\Rightarrow d+d'=d'+\dfrac{d'f}{d'-f}=\dfrac{d'^2-d'f+d'f}{d'-f}=\dfrac{d'^2}{d'-f}\)
\(\left(d+d'\right)_{min}\Leftrightarrow(\dfrac{1}{d'}-\dfrac{f}{d'^2})_{max}\)
Dat \(\dfrac{1}{d'}=a\Rightarrow a-a^2f=-\left(a^2f+a+\dfrac{1}{4f}\right)+\dfrac{1}{4f}=-\left(a\sqrt{f}+\dfrac{1}{2\sqrt{f}}\right)^2\le\dfrac{1}{4f}\)
\("="\Leftrightarrow a\sqrt{f}=\dfrac{1}{2\sqrt{f}}\Leftrightarrow2af=1\Rightarrow a=\dfrac{1}{2f}\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{2f}\Rightarrow d'=2f\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{2f^2}{2f-f}=2f\)
\(\Rightarrow\left(d+d'\right)_{min}=2f+2f=4f\Rightarrow D.4f\)
8/ \(D=\dfrac{1}{f}=-\dfrac{1}{20}=-0,05\left(dp\right)\Rightarrow C.-0,05dp\)
15/ \(k_1=\dfrac{f}{f-d_1};k_2=\dfrac{f}{f-d_2};\dfrac{k_1}{k_2}=-1\)
\(d_2=d_1-12\Rightarrow\dfrac{k_1}{k_2}=-1=\dfrac{f-d_2}{f-d_1}=\dfrac{f-d_1-12}{f-d_1}\) (1)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};-\dfrac{d'_1}{d_1}=3\Rightarrow\dfrac{1}{f}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\)
\(\Rightarrow\dfrac{1}{f}=\dfrac{2}{3d_1}\Rightarrow d_1=\dfrac{2}{3}f\)
Thay vo (1)\(\Rightarrow\dfrac{f-\dfrac{2}{3}f-12}{f-\dfrac{2}{3}f}=-1\Leftrightarrow\dfrac{1}{3}f-12=-\dfrac{1}{3}f\Rightarrow f=18\left(cm\right)\)
19/ \(\sin i=n\sin r=n\cos i\Rightarrow\tan i=n\Rightarrow A.\tan i=n\)
22/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(-d'-d=45\Rightarrow d'=-d-45\Rightarrow\dfrac{1}{20}=\dfrac{1}{d}-\dfrac{1}{d+45}\)
\(\Leftrightarrow d^2+45d=45.20\Leftrightarrow\left[{}\begin{matrix}d=15\left(cm\right)\\d=-60\left(loai\right)\end{matrix}\right.\Rightarrow d'=-60\left(cm\right)\)
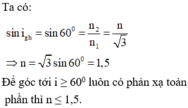
Chọn đáp án A.