Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để quả bóng ở độ cao trên 5m so với mặt đất thì:
\(\begin{array}{l}h(t) > 5\\ \Rightarrow - 4,9{t^2} + 20t + 1 > 5\\ \Rightarrow - 4,9{t^2} + 20t - 4 > 0\end{array}\)
Đặt \(f(t) = - 4,9{t^2} + 20t - 4\)có \(\Delta ' = b{'^2} - ac = {10^2} - ( - 4,9).( - 4) = 80,4 > 0\)nên \(f(t)\)có 2 nghiệm: \(\begin{array}{l}{t_1} = \frac{{ - b' + \sqrt {\Delta '} }}{a} = \frac{{ - 10 + \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 - \sqrt {80,4} }}{{4,9}}\\{t_2} = \frac{{ - b' - \sqrt {\Delta '} }}{a} = \frac{{ - 10 - \sqrt {80,4} }}{{ - 4,9}} = \frac{{10 + \sqrt {80,4} }}{{4,9}}\end{array}\)
Mặt khác \(a = - 4,9 < 0\), do đó ta có bảng xét dấu sau

Do đó để \(h(t) > 5\)thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)
Vậy để quả bóng sẽ ở độ cao trên 5m so với mặt đất thì \(t \in \left( {\frac{{10 - \sqrt {80,4} }}{{4,9}};\frac{{10 + \sqrt {80,4} }}{{4,9}}} \right)\)

Theo giả thiết, khoảng thời gian bóng nằm ở độ cao 40 m là nghiệm của bất phương trình sau:
\(\begin{array}{l}h\left( t \right) > 40 \Leftrightarrow - 4,9{t^2} + 30t + 2 > 40\\ \Leftrightarrow - 4,9{t^2} + 30t - 38 > 0\end{array}\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 30t - 38\) có \(\Delta = 155,2 > 0\), có hai nghiệm phân biệt là \({x_1} \simeq 1,8;{x_2} \simeq 4,3\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
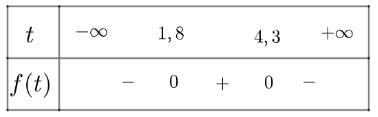
Từ đó cho thấy khoảng từ 1,8 s đến 4,3 s lag khoảng thời gian bóng cao so với mặt đất lớn hơn 40 m
Vậy quả bóng nằm ở độ cao trên 40 m trong thời gian 2,5 giây.

a) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 7 \Leftrightarrow - 4,9{t^2} + 10t - 5,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 5,4\) có \(\Delta = - \frac{{146}}{{25}} < 0\) và \(a = - 4,9 < 0\)
nên \(f\left( x \right)\) âm với mọi t, suy ra bât phương trình \( - 4,9{t^2} + 10t + 1,6 > 7\) vô nghiệm
vậy bóng không thể cao trên 7 m
b) Theo giả thiết ta có bất phương trình sau: \( - 4,9{t^2} + 10t + 1,6 > 5 \Leftrightarrow - 4,9{t^2} + 10t - 3,4 > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 10t - 3,4\) có hai nghiệm phân biệt là \({t_1} \simeq 0,43;{t_2} \simeq 1,61\) và \(a = - 4,9 < 0\)
nên \(f\left( t \right)\) dương khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)
Vậy khi t nằm trong khoảng \(\left( {0,43;1,61} \right)\)giây thì bóng ở độ cao trên 5 m

a) Để viên bi chạm đất thì \(\begin{array}{l}h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\\ \Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\end{array}\)
Do \(t \ge 0\) nên t=2(s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\)
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\)
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\)

a. Ta có: \(sin\left(30t\right)\le1\)
\(\Leftrightarrow3sin\left(30t\right)\le3\)
\(\Leftrightarrow5+3sin\left(30t\right)\le8\)
Vậy độ sâu mực nước lớn nhất tại bến cảng đó là 8(m)
b. Ta có: \(8\ge h\ge6,5\) \(\Leftrightarrow8\ge5+3sin\left(30t\right)\ge6,5\)\(\Leftrightarrow3\ge3sin\left(30t\right)\ge1,5\)
\(\Leftrightarrow1\ge sin\left(30t\right)\ge0,5\)\(\Leftrightarrow\dfrac{\pi}{2}\ge30t\ge\dfrac{\pi}{6}\)\(\Leftrightarrow\dfrac{\pi}{60}\ge t\ge\dfrac{\pi}{180}\)
Vậy sau giữa trưa từ \(\dfrac{\pi}{180}\) (giờ) đến \(\dfrac{\pi}{60}\)(giờ) thuyền có thể vào bến cảng

a) Đặt phương trình parabol là \(\left( P \right):h = a{t^2} + bt + c\)
Ta có quả bóng được đá lên từ điểm A(0; 0,2) nên \(0,2 = c\)
Ta có quả bóng đạt độ cao 8,5 m sau 1 giây có nghĩa là tại t=1 thì h=8,5. Khi đó
\(8,5 = a + b+0,2 \Leftrightarrow a+b = 8,3\) (1)
Ta có quả bóng đạt độ cao 6 m sau 2 giây có nghĩa là tại t=2 thì h=6.
=> \(6 = a{.2^2} + b.2+0,2 \)\( \Leftrightarrow 2a + b = 2,9\) (2)
Từ (1) và (2) ta được hệ \(\left\{ \begin{array}{l}a + b = 8,3\\2a + b = 2,9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 5,4\\b = 13,7 \end{array} \right.\)
Vậy \(\left( P \right):h = - 5,4{t^2} + 13,7t+0,2\)
b) Để quả bóng không chạm đất thì \(h > 0\)
\(\Leftrightarrow - 5,4{t^2} + 13,7t+0,2 > 0\)
PT \(- 5,4{t^2} + 13,7t+0,2 = 0\) có hai nghiệm xấp xỉ là \(t_1 = -0,0145\) và \(t_2 = 2,55\)
Sử dụng định lí về dấu, ta có \(h>0\) khi \(t_1 <t< t_2\) suy ra \(0<t<2,55\) (vì t>0)
Vậy trong khoảng thời gian từ lúc đá đến thời gian \(t = 2,55\) thì quả bóng chưa chạm đất.

a) Vị trí ban đầu ứng với \(t = 0\), suy ra vật thể ở vị trí có tọa độ là \(A\left( {2;5} \right)\).
Vị trí kết thúc ứng với \(t = 180\) , suy ra vật thể ở vị trí có tọa độ là \(B\left( {2;3} \right)\).
b) Từ đẳng thức \({\left( {\sin {t^o}} \right)^2} + {\left( {\cos {t^o}} \right)^2} = 1\) ta suy ra \({\left( {{x_M} - 2} \right)^2} + {\left( {{y_M} - 4} \right)^2} = 1\)
Do đó, M thuộc đường tròn \(\left( C \right)\) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 4} \right)^2} = 1\)
Đường tròn có tâm \(I\left( {2;4} \right)\), bán kính \(R = 1\) và nhận AB làm đường kính.
Khi \(t \in \left[ {0;180} \right]\) thì \(\sin t \in \left[ {0;1} \right]\) và \(\cos t \in \left[ { - 1;1} \right]\). Do đó, \(2 + \sin {t^o} \in \left[ {2;3} \right]\) và \(4 + \cos {t^o} \in \left[ {3;5} \right]\).
Vậy quỹ đạo của vật thể là nửa đường tròn đường kính AB vẽ trên nửa mặt phẳng chứa điểm \(C\left( {3;0} \right)\) bờ AB.

Khoảng thời gian cá heo ở trên không chính khoảng cá heo cao hơn mặt nước
Ta có bất phương trình \(h\left( t \right) > 0 \Leftrightarrow - 4,9{t^2} + 9,6t > 0\)
Xét tam thức \(f\left( t \right) = - 4,9{t^2} + 9,6t\) có \(\Delta = 92.16 > 0\), có hai nghiệm phân biệt là \({x_1} = 0,{x_2} = \frac{{96}}{{49}}\) và có \(a = - 4,9 < 0\)
Ta có bảng xét dấu như sau:
Vậy khoảng thời gian cá heo ở trên không là khoảng \(\left( {0;\frac{{96}}{{49}}} \right)\) giây