Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số có đồ thị là một hình parabol, bề lõm quay xuống dưới.
Hình ảnh hình học có tính đối xứng.

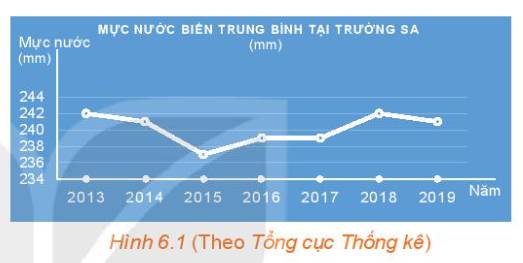
a, Thời gian theo dõi mực nước ở Trường Sa được thể hiện trong hình từ năm 2013 đến năm 2019.
b, Trong khoảng thời gian đó, năm 2015 mực nước biển trung bình của Trường Sa là thấp nhất (khoảng 237mm), còn năm 2013 và năm 2018 thì là năm có mực nước biển của Trường Sa là cao nhất (khoảng 242mm)

Sự khác biệt là:
- Đơn vị đo: tấn và 500.
- Khối lượng hàng là đại lượng chỉ có độ lớn (500 tấn), còn độ dịch chuyển của tàu là đại lượng có cả độ lớn (500 km) và hướng (từ A đến B).

Sau 2 giờ, tàu thứ nhất đã đi được `25.2 = 50` hải lý.
Sau 2 giờ, tàu thứ hai đã đi được `20.2 = 40` hải lý.
Với a = `50` hải lý, b = `40` hải lý và `C = 180° - (15° + 32°) = 133°`, ta có:
`c^2 = 50^2 + 40^2 - 2.50.40.cos(133°)`
=> `c^2 ≈ 2500 + 1600 - 4000.(-0.6428) ≈ 4107.14`
Vậy, khoảng cách giữa hai tàu sau 2 giờ là:
`c ≈ √4107.14 ≈ 64,07 hải lý`

Ta có giá trị trung bình:
\(\overline x = \frac{0,398 + 0,399 + 0,408 + 0,410 + 0,406 + 0,405 + 0,402}{7}\)
\( = 0,404\)
Ta có bảng sau:
Giá trị | Độ lệch | Bình phương độ lệch |
0,398 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,399 | 0,005 | \(2,{5.10^{ - 5}}\) |
0,408 | 0,004 | \(1,{6.10^{ - 5}}\) |
0,410 | 0,006 | \(3,{6.10^{ - 5}}\) |
0,406 | 0,002 | \(0,{4.10^{ - 5}}\) |
0,405 | 0,001 | \(0,{1.10^{ - 5}}\) |
0,402 | 0,002 | \(0,{4.10^{ - 5}}\) |
Tổng | \(12,{2.10^{ - 5}}\) |
Phương sai:
\({s^2} = \frac{{12,{{2.10}^{ - 5}}}}{7} \approx 0,000017\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} \approx 4,{17.10^{ - 3}}\)
Phép đo có độ chính xác cao.

a. Ta có: \(sin\left(30t\right)\le1\)
\(\Leftrightarrow3sin\left(30t\right)\le3\)
\(\Leftrightarrow5+3sin\left(30t\right)\le8\)
Vậy độ sâu mực nước lớn nhất tại bến cảng đó là 8(m)
b. Ta có: \(8\ge h\ge6,5\) \(\Leftrightarrow8\ge5+3sin\left(30t\right)\ge6,5\)\(\Leftrightarrow3\ge3sin\left(30t\right)\ge1,5\)
\(\Leftrightarrow1\ge sin\left(30t\right)\ge0,5\)\(\Leftrightarrow\dfrac{\pi}{2}\ge30t\ge\dfrac{\pi}{6}\)\(\Leftrightarrow\dfrac{\pi}{60}\ge t\ge\dfrac{\pi}{180}\)
Vậy sau giữa trưa từ \(\dfrac{\pi}{180}\) (giờ) đến \(\dfrac{\pi}{60}\)(giờ) thuyền có thể vào bến cảng