Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Xác định A, ω và φ của phương trình x = Acos(ωt + φ)
Sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.
Cách giải:
+ Biên độ dao động: A = R = 8cm
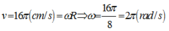
+ Tốc độ:
+ Chất điểm bắt đầu từ vị trí thấp nhất của đường tròn theo chiều ngược chiều kim đồng hồ:
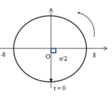
= Pha ban đầu: φ = -π/2
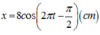
= Phương trình:

Chu kì: T = 2π: π = 2s
Hình chiếu P sẽ dao động điều hòa với biên độ 30cm.
Thời gian t = 3s = 3. T/2
Trong mỗi nửa chu kì, quãng đường P đi được là 2A.
Quãng đường mà hình chiếu P đi được trong 3s là: 3.2A = 6A = 180cm.
Tốc độ trung bình: v = S : t = 180 : 3 = 60 cm/s

Tốc độ lớn nhất hay nhỏ nhất ứng với quãng đường lớn nhất và nhỏ nhất.
Chu kì dao động của P: \(T=2\pi/\omega=4s\)
\(t=1s=T/4\), trong thời gian này chất điểm M quay một góc là: \(360/4=90^0\)
+ P có quãng đường lớn nhất ứng với chuyển động quanh VTCB, mỗi bên 1 góc \(45^0\), quãng đường: \(S=2.4.\cos 45^0=4\sqrt 2(cm)\)
\(\Rightarrow v = 4\sqrt 2(cm/s)\)
+ P có quãng đường nhỏ nhất ứng với chuyển động quanh biên, mỗi bên 1 góc \(45^0\), quãng đường:
\(S=2.(4-4.\cos45^0)=8-4\sqrt 2(cm)\)
\(\Rightarrow v = 8-4\sqrt 2 cm\)

Đáp án B
+ Hình chiếu của chất điểm này là một dao động điều hòa → tốc độ cực đại v max = ωA = 50 cm/s.

Đáp án D
+ Tốc độ cực đại của hình chiếu chất điểm lên Ox là
![]()

Đáp án C
Hình chiếu của chuyển động tròn đều trên trục ngang Ox chính là dao động điều hòa => Bán kính R cũng chính là biên độ A = 10(cm) và tốc độ góc quay là ω = 5(rad/s)
=> Tốc độ cực đại của hình chiếu lên trục Ox là: vmax = ωA = 5.10 = 50 (cm/s)

Đáp án B
Ta có T = 2π/ω = 2 s và A = 10 cm
Tại t = 0, x = 0 cm; Δt = 1 s = T/2 → ΔS = 2A = 20 cm

Tần số góc: \(\omega = 10\pi (rad/s)\)
Chu kì: \(T = \frac{2\pi}{\omega} = \frac{2\pi}{10\pi} = 0,2 (s)\)

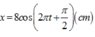
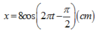
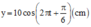
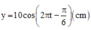
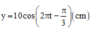
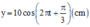
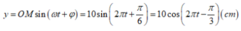
Đáp án D
Phương pháp: Sử dụng lí thuyết về phương trình dao động điều hoà
Cách giải:
Biên độ dao động: A = 8cm
Ta có: v = ωA=16π cm/s =>ω = 2π (rad/s)
Chất điểm bắt đầu đi từ vị trí thấp nhất của đường tròn, vậy pha ban đầu là φ = –π/2 (rad)
=> x = 8 cos 2 πt - π 2