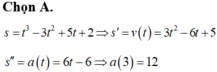Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

a) Ta có:
v(t) = s’(t) = t3 – 3t2 + t – 3
a(t) = s’’(t) = 3t2 – 6t + 1
Do đó: v(2) = -5; a(2) = 1
b) v(t) = 0 ⇔ t3 – 3t2 + t – 3
⇔ t = 3
Vậy t = 3
Theo ý nghĩa cơ học của đạo hàm ta có:
v(t)=s'(t)=t3-3t2+t-3
v(2)=23-3.22+2-3=-5 (m/s)
a(t)=v'(t)=s''(t)=3t2-6t+1
a(2)=3.22-6.2+1=1 (m/s2)
v(t)=t3-3t2+t-3=0
(t-3)(t1+1)=0 t = 3
Vậy thời điểm to=3s thì vận tốc bằng 0.

\(y'=x^2-\left(3m+2\right)x+2m^2+3m+1\)
\(\Delta=\left(3m+2\right)^2-4\left(2m^2+3m+1\right)=m^2\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\frac{3m+2+m}{2}=2m+1\\x_2=\frac{3m+2-m}{2}=m+1\end{matrix}\right.\)
Để hàm số có cực đại, cực tiểu \(\Rightarrow x_1\ne x_2\Rightarrow m\ne0\)
- Nếu \(m>0\Rightarrow2m+1>m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=m+1\\x_{CT}=2m+1\end{matrix}\right.\)
\(\Rightarrow3\left(m+1\right)^2=4\left(2m+1\right)\) \(\Rightarrow3m^2-2m-1=0\Rightarrow\left[{}\begin{matrix}m=1\\m=-\frac{1}{3}< 0\left(l\right)\end{matrix}\right.\)
- Nếu \(m< 0\Rightarrow m+1>2m+1\Rightarrow\left\{{}\begin{matrix}x_{CĐ}=2m+1\\x_{CT}=m+1\end{matrix}\right.\)
\(\Rightarrow3\left(2m+1\right)^2=4\left(m+1\right)\Rightarrow12m^2+8m-1=0\)
\(\Rightarrow\left[{}\begin{matrix}m=\frac{-2+\sqrt{7}}{6}>0\left(l\right)\\m=\frac{-2-\sqrt{7}}{6}\end{matrix}\right.\) \(\Rightarrow\sum m=\frac{4-\sqrt{7}}{6}\)

\(v\left(t\right)=s'\left(t\right)=3t^2+8t\)
\(a\left(t\right)=v'\left(t\right)=6t+8\)
Tại thời điểm vận tốc của vật bằng 11
\(\Leftrightarrow3t^2+8t=11\Leftrightarrow3t^2+8t-11=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{11}{3}< 0\left(l\right)\end{matrix}\right.\)
\(\Rightarrow a=6.1+8=14\left(m/s^2\right)\)

Ta có: \(x^2+2xy+7(x+y)+2y^2+10=0\)
<=> \((x^2+2xy+y^2)+7(x+y)+y^2+10=0\)
<=>(1)
Đặt t=x+y
=>(1)<=>\(y^2+t^2+7t+10=0
\)
Phương trình có nghiệm khi \(\Delta\)'\(\ge\)0
<=>\(t^2+7t+10=0
\) \(\le\)0
<=> -5\(\le\)t\(\le\)-2
=>Max S=1 khi t=-2<=>y=0;x=-2
Min S=-2 khi t=-5<=>y=0;x=-5