Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có phải là trọng lượng riêng của nước biển là 10300 \(N\)/\(m^3\)
và trọng lượng riêng của xăng là \(7000N\)/\(m^3\)
Với lại là tìm độ cao của cột xăng chứ tính cột nước thì bao nhiêu chả được.
Tóm tắt.
\(h'=20cm\)
\(d_1=10300N\)/\(m^3\)
\(d_2=7000N\)/\(m^3\)
_____________
\(h=?\)
Giải

Xét A là điểm nằm ở đáy cột xăng và B là điểm nằm cùng một mặt phẳng nằm ngang với điểm A (Trong lòng cột nước biển)
Ta có: \(p_A=p_B\) và \(h_1+h'=h\Rightarrow h_1+20=h\)
\(\Rightarrow d_1.h=d_2.h_1\Rightarrow d_1.\left(h_1+h'\right)=d_2.h_1\Rightarrow7000\left(h_1+20\right)=10300.h_1\)
\(\Rightarrow7000h_1+140000=10300h_1\Rightarrow140000=3300h_1\Rightarrow h_1\approx42\left(cm\right)\)

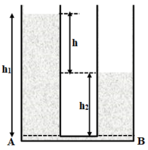
Giả sử ta đổ xăng vào nhánh bên trái, khi đó chiều cao của cột xăng là h1, nước bên trong ống bên phải dâng lên có độ cao là h2.
Ta có: h = 18mm = 0,018m; d1 = 7000N/m3; d2 = 10300 N/m3.
Xét hai điểm A và B trong hai nhánh nằm trong cùng một mặt phẳng ngang trùng với mặt phân cách giữa xăng và nước biển.
Ta có: pA = pB mà pA = d1.h1; pB = d2.h2;
Suy ra: d1.h1 = d2.h2;
Theo hình vẽ thì h2 = h1 – h, do đó:
d1.h1 = d2.(h1 – h) = d2.h1 – d2.h
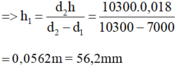

Giả sử chiều cao cột xăng là h1, h = 18mm = 0,018m
Ta có
\(p_1=d_1h_1\\ p_2=d_2h_2\\ d_1h_1=d_2h_2\\ d_1h_1=d_2\left(h_1-h\right)\\ \Rightarrow h_1=\dfrac{d_2h}{d_2-d_1}=\dfrac{10300.0,018}{10300-7000}=0,056=56mm\)
Gọi trọng lượng riêng của xăng là d1, trọng lượng riêng của nước biển là d2, dộ chênh lệch giữa 2 nhánh là h1
Xét 2 điểm A & B nằm cùng trên 1 mặt phẳng ngang ngăn cách giữa nước và xăng
Có pA = pB => h.d1 = d2(h - h1)
=> h: (h-h1) = d2:d1 = 10300 : 7000 = 103:70
=> h.70 = 103.( h-h1)
= 103.h - 103. 18 = 103h - 1854
=> 33h = 1854 => h = 1854: 33= 56,2(mm)