mong mọi người lm giúp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mong mọi người có thể lm hộ bài 4 .
NV
14 tháng 7 2016
5x2 - 4(x2 - 2x + 1) - 5 = 0
=> 5x2 - 4x2 + 8x - 4 - 5 = 0
=> x2 + 8x - 9 = 0
=> x2 + 9x - x - 9 = 0
=> x(x + 9) - (x + 9) = 0
=> (x + 9)(x - 1) = 0
=> x + 9 = 0 => x = -9
hoặc x - 1 = 0 = > x = 1
Vậy x = -9, x = 1
14 tháng 7 2016
\(5x^2-4\left(x^2-2x+1\right)-5=0\)
\(\left(5x^2-5\right)-4\left(x^2-2.1.x+1^2\right)=0\)
\(5\left(x^2-1\right)-4\left(x-1\right)^2=0\)
\(5\left(x-1\right)\left(x+1\right)-4\left(x-1\right)\left(x-1\right)=0\)
\(\left[5\left(x+1\right)-4\left(x-1\right)\right]\left(x-1\right)=0\)
\(\left(5x+5-4x+4\right)\left(x-1\right)=0\)
\(\left(x+9\right)\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+9=0\\x-1=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-9\\x=1\end{cases}}\)
Vậy \(\orbr{\begin{cases}x=-9\\x=1\end{cases}}.\)
19 tháng 11 2023
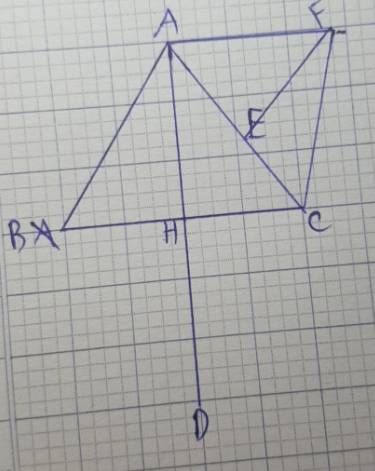
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
10 tháng 10 2021
\(x^4+324=\left(x^4+36x^2+324\right)-36x^2\)
\(=\left(x^2+18\right)^2-36x^2\)
\(=\left(x^2-6x+18\right)\left(x^2+6x+18\right)\)
TN
14 tháng 7 2016
a)xm+4+xm+3-x-1
=(xm+4-x)+(xm+3-1)
=x(xm+3-1)+(xm+3-1)
=(x+1)(xm+3-1)
Với x=-2 ta có:... bn tự thay
b)x6-x4+2x3+2x2=x6-2x5+2x4+2x5-4x4+4x3+x4-2x3+2x2
=x4(x2-2x+2)+2x3(x2-2x+2)+x2(x2-2x+2)
=(x4+2x3+x2)(x2-2x+2)
=[x2(x2+2x+1)](x2-2x+2)
=x2(x+1)2(x2-2x+2)
Với x=-2 bn tự thay nhé h mk bận
16 tháng 10 2021
\(1,=3x\left(x-2\right)\\ 2,=2xy\left(1+z\right)\\ 3,=3x^2y\left(5-3y\right)\\ 4,=\left(2x+1\right)\left(4x^2-2x+1\right)\\ 5,=4\left(x^2-4\right)=4\left(x-2\right)\left(x+2\right)\\ 6,=\left(x-y\right)\left(x-y\right)=\left(x-y\right)^2\\ 7,=\left(x-1\right)\left(x+y\right)\\ 8,=2xy\left(x+2y\right)\\ 10,=\left(x-3\right)\left(x^2+3x+9\right)\)
30 tháng 12 2021
a: Xét tứ giác OAMD có
OA//MD
OD//AM
Do đó: OAMD là hình bình hành
mà \(\widehat{AOD}=90^0\)
nên OAMD là hình chữ nhật
24 tháng 10 2021
Bài 2:
\(\left\{{}\begin{matrix}Z-N=-1\\2Z-N=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-Z=-13\\Z-N=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}Z=13\\N=14\end{matrix}\right.\)
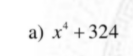
Gọi khối lượng táo và xoài lần lượt là a,b
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=14\\80000a+50000b=820000\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=10\end{matrix}\right.\)