K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
21 tháng 12 2019
Vì các học sinh lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh nên số học sinh của lớp là: 30 + 25 - 16 = 39 (học sinh).
Chọn C.
16 tháng 5 2022
Vì các học sinh lớp 10A1 đều học giỏi ít nhất một trong hai môn Toán hoặc Tiếng Anh nên số học sinh của lớp là: 30 + 25 - 16 = 39 (học sinh).
CM
18 tháng 10 2018
Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
⇒ p = C 4 2 C 40 2 = 1 130
CM
1 tháng 12 2019
Xác suất để 2 học sinh tên Anh lên bảng là C 4 2 C 40 2 = 1 130
Chọn đáp án A.
CM
12 tháng 9 2018
Đáp án C
Cách giải:
Gọi ngẫu nhiên hai học sinh lên bảng trong 40 học sinh nên ta có: n Ω = C 40 2 = 780
Gọi biến cố A: “Trong hai bạn được gọi lên bảng, cả hai bạn đều tên là Anh”.
Trong lớp có 4 bạn tên là Anh nên ta có: n A = C 2 2 . C 4 2 = 6
Khi đó ta có xác suất để hai bạn được gọi lên bảng đều tên là Anh là:
P A = n A n Ω = 6 780 = 1 130
CM
4 tháng 6 2018
Đáp án A
Cách gọi ngẫu nhiên 2 học sinh lên bảng: C 40 2
Cách gọi 2 học sinh tên Anh lên bảng: C 4 2
=> p = C 4 2 C 40 2 = 1 130
CM
4 tháng 9 2019
Đáp án B
Gọi A là biến cố “học sinh đăng ký Toán”
Gọi B là biến cố “học sinh đăng ký Lý”
A ∩ B “học sinh đăng ký Toán, Lý”
A ∪ B là biến cố “học sinh có đăng ký học phụ đạo”
P ( A ∪ B ) = P ( A ) + P ( B ) - P ( A ∩ B ) = 38 50 + 30 50 - 25 50 = 43 50
A ∪ B là biến cố “học sinh không đăng ký môn nào cả”
P A ∪ B = 1 - Q A ∪ B = 8 50 = 0 , 14
CM
11 tháng 3 2019
Đáp án B
Phương pháp: Xác suất :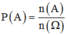 
Cách giải:
Số phần tử của không gian mẫu : 
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó : 
Xác suất cần tìm:
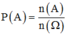
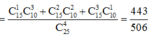
không có môn sinh học lớp mẫu giáo nhé bạn