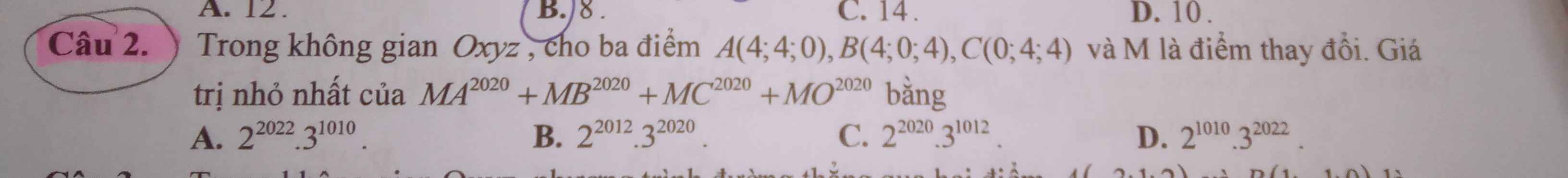K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2022
Dễ dàng nhận ra tứ diện OABC là tứ diện đều \(\Rightarrow MA^{2020}+MB^{2020}+MC^{2020}+MO^{2020}\) đạt min khi M trùng trọng tâm tứ diện
Khi đó \(M\left(2;2;2\right)\Rightarrow MA=MB=MC=MO=\sqrt{2^2+2^2+2^2}=2\sqrt{3}\)
\(\Rightarrow P=4.\left(2\sqrt{3}\right)^{2020}=2^{2022}.3^{1010}\)
DN
13 tháng 4 2022
Thầy ơi thầy giúp em bài này với ạ https://hoc24.vn/cau-hoi/1-limlimits-xrightarrow1dfracx-sqrtx2x-3sqrt3x22-cho-hinh-chop-sabcd-co-day-la-hinh-chu-nhat-ab-a-ad-2a-sa-vuong-goc-voi-day-va-sa-aa-cm-cdperpleftsadright.5799562370088
Em cảm ơn ạ
TH
1
KR
28 tháng 1 2023
\(I=\int\dfrac{2}{2+5sinxcosx}dx=\int\dfrac{2sec^2x}{2sec^2x+5tanx}dx\\ =\int\dfrac{2sec^2x}{2tan^2x+5tanx+2}dx\)
We substitute :
\(u=tanx,du=sec^2xdx\\ I=\int\dfrac{2}{2u^2+5u+2}du\\ =\int\dfrac{2}{2\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{8}}du\\ =\int\dfrac{1}{\left(u+\dfrac{5}{4}\right)^2-\dfrac{9}{16}}du\\ \)
Then,
\(t=u+\dfrac{5}{4}\\I=\int\dfrac{1}{t^2-\dfrac{9}{16}}dt\\ =\int\dfrac{\dfrac{2}{3}}{t-\dfrac{3}{4}}-\dfrac{\dfrac{2}{3}}{t+\dfrac{3}{4}}dt\)
Finally,
\(I=\dfrac{2}{3}ln\left(\left|\dfrac{t-\dfrac{3}{4}}{t+\dfrac{3}{4}}\right|\right)+C=\dfrac{2}{3}ln\left(\left|\dfrac{tanx+\dfrac{1}{2}}{tanx+2}\right|\right)+C\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2021
\(y'=3mx^2-4mx-\left(m+1\right)\)
- Với \(m=0\Rightarrow y'=-1< 0\) hàm nghịch biến trên R (thỏa)
- Với \(m\ne0\) hàm nghịch biến trên R khi:
\(\left\{{}\begin{matrix}3m< 0\\\Delta'=4m^2+3m\left(m+1\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\7m^2+3m\le0\\\end{matrix}\right.\)
\(\Leftrightarrow-\dfrac{3}{7}\le m< 0\)
Vậy \(-\dfrac{3}{7}\le m\le0\Rightarrow m=0\)
S có 1 phần tử
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Bài 5:
\(y=m\sqrt{x^2-4x+7}-(3x-4)=\frac{(m^2-9)x^2+(24-4m^2)x+(7m^2-16)}{m\sqrt{x^2-4x+7}+3x-4}\)
Để đths $y$ có TCN thì:\(\lim\limits_{x\to \pm \infty}y\) hữu hạn
Để điều này xảy ra thì $m^2-9=0\Leftrightarrow m=\pm 3$
Kiểm tra lại thấy cả 2 giá trị này đều thỏa mãn.
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Bài 6: Tiệm cận của ĐTHS chứ làm gì có tiệm cận hàm số hả bạn?
a.
\(y=\frac{x^2-3x+2}{2x^2+x-1}=\frac{x^2-3x+2}{(2x-1)(x+1)}\)
$(2x-1)(x+1)=0\Leftrightarrow x=\frac{1}{2}$ hoặc $x=-1$
Do đó TCĐ của ĐTHS là $x=\frac{1}{2}$ và $x=-1$
Mặt khác: \(\lim\limits_{x\to \pm \infty}\frac{x^2-3x+2}{2x^2+x-1}=\frac{1}{2}\) nên $y=\frac{1}{2}$ là TCN của ĐTHS.
b.
$x+1=0\Leftrightarrow x=-1$ nên $x=-1$ là TCĐ của đths
$\lim\limits_{x\to \pm \infty}\frac{1-x}{1+x}=-1$ nên $y=-1$ là TCN của đths
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)
PT
25 tháng 5 2016
bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với