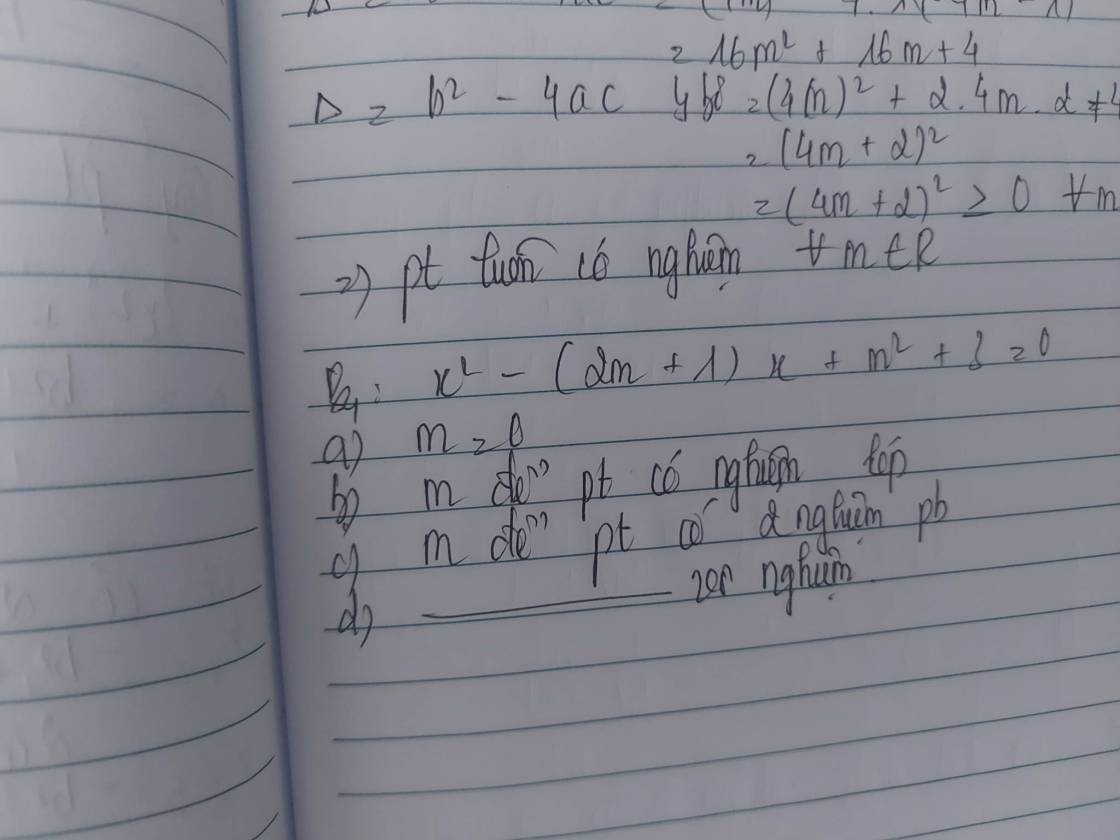K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 7 2023
a: Xét tứ giác ACBD có
AB cắt CD tại trung điểm của mỗi đường
AB=CD
=>ACBD là hình chữ nhật
b: Xét ΔABF có AO/AB=AQ/AF=1/2
nên QO//BF
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
14 tháng 12 2021
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
14 tháng 12 2021
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
2
20 tháng 2 2023
`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)
`=>m=0` ptr vô nghiệm
`b)` Ptr có nghiệm kép `<=>\Delta=0`
`<=>[-(2m+1)]^2-4(m^2+3)=0`
`<=>4m^2+4m+1-4m^2-12=0`
`<=>4m-11=0`
`<=>m=11/4`
`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`
`<=>4m-11 > 0<=>m > 11/4`
`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`
20 tháng 2 2023
Bài 2:
a: Khi m=0 thì pt sẽ là:
\(x^2-x+3=0\)
=>\(x\in\varnothing\)
b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)
=4m^2+4m+1-4m^2-12
=4m-11
Để pt có nghiệm kép thì 4m-11=0
=>m=11/4
c: Để phương trình có hai nghiệm pb thì 4m-11>0
=>m>11/4
d: Để pt vô nghiệm thì 4m-11<0
=>m<11/4
NA
1
19 tháng 7 2021
Bài 2:
a) Để hàm số đồng biến thì m+1>0
hay m>-1
b) Để hàm số đi qua điểm A(2;4) thì
Thay x=2 và y=4 vào hàm số, ta được:
\(\left(m+1\right)\cdot2=4\)
\(\Leftrightarrow m+1=2\)
hay m=1
c) Để hàm số đi qua điểm B(2;-4) thì
Thay x=2 và y=-4 vào hàm số, ta được:
\(2\left(m+1\right)=-4\)
\(\Leftrightarrow m+1=-2\)
hay m=-3
19 tháng 7 2021
Bài 1:
b) Ta có: \(5\cdot\sqrt{25a^2}-25a\)
\(=5\cdot5\cdot\left|a\right|-25a\)
\(=-25a-25a=-50a\)
NA
2
Y
17 tháng 1 2023
\(c,\left\{{}\begin{matrix}\dfrac{2}{x-2}+\dfrac{1}{y+1}=3\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x-2}+\dfrac{2}{y+1}=6\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{y+1}+\dfrac{3}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{y+1}=5\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+1=1\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=0\left(2\right)\\\dfrac{4}{x-2}-\dfrac{3}{y+1}=1\left(1\right)\end{matrix}\right.\)
Thay \(\left(2\right)\) vào \(\left(1\right)\) :
\(\dfrac{4}{x-2}-\dfrac{3}{0+1}=1\)
\(\Rightarrow\dfrac{4}{x-2}-3=1\)
\(\Rightarrow\dfrac{4}{x-2}=4\)
\(\Rightarrow x-2=1\)
\(\Rightarrow x=3\)
Vậy hệ phương trình có nghiệm duy nhất \(\left(x;y\right)=\left(3;0\right)\)
17 tháng 1 2023
c: =>4/x-2+2/y+1=6 và 4/x-2-3/y+1=1
=>5/y+1=5 và 2/x-2+1/y+1=3
=>y+1=1 và 2/x-2+1=3
=>y=0 và x-2=1
=>x=3 và y=0
TT
1
