
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.
\(\Leftrightarrow cos2x-cos8x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow2sin5x.sin3x-sin3x+cos5x-2sin5x.cos5x=0\)
\(\Leftrightarrow sin3x\left(2sin5x-1\right)-cos5x\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left(sin3x-cos5x\right)\left(2sin5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos5x=sin3x=cos\left(\dfrac{\pi}{2}-3x\right)\\sin5x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{\pi}{2}-3x+k2\pi\\5x=3x-\dfrac{\pi}{2}+k2\pi\\5x=\dfrac{\pi}{6}+k2\pi\\5x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{16}+\dfrac{k\pi}{4}\\x=-\dfrac{\pi}{4}+k\pi\\x=\dfrac{\pi}{30}+\dfrac{k2\pi}{5}\\x=\dfrac{\pi}{6}+\dfrac{k2\pi}{5}\end{matrix}\right.\)
3.
\(\Leftrightarrow1+sinx=cosx-cos3x+2sinx.cosx+1-2sin^2x\)
\(\Leftrightarrow sinx=2sin2x.sinx+2sinx.cosx-2sin^2x\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\Rightarrow x=k\pi\\1=2sin2x+2cosx-2sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow4sinx.cosx+2cosx-2sinx-1=0\)
\(\Leftrightarrow2cosx\left(2sinx+1\right)-\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2cosx+1\right)\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\cosx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow...\)

1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)


17.
Gọi số vi khuẩn ban đầu là x
Sau 5 phút số vi khuẩn là: \(x.2^5=64000\Rightarrow x=2000\)
Sau k phút:
\(2000.2^k=2048000\Rightarrow2^k=1024=2^{10}\)
\(\Rightarrow k=10\)
18.
\(S_{2019}=\left(\dfrac{1}{2}\right)^1+1+\left(\dfrac{1}{2}\right)^2+1+...+\left(\dfrac{1}{2}\right)^{2019}+1\)
\(=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}+2019\)
Xét \(S=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}\) là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=\dfrac{1}{2}\\n=2019\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{2}.\dfrac{\left(\dfrac{1}{2}\right)^{2019}-1}{\dfrac{1}{2}-1}=1-\dfrac{1}{2^{2019}}\)
\(\Rightarrow S_{2020}=2019+S=2020-\dfrac{1}{2^{2019}}\)
19. C là khẳng định sai, ví dụ: \(u_n=2\) ; \(v_n=-\dfrac{1}{n}\)

\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt[3]{x-2}+1}{\sqrt[]{x+3}-2}=\lim\limits_{x\rightarrow1}\dfrac{\left(\sqrt[3]{x-2}+1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)\left(\sqrt[]{x+3}+2\right)}{\left(\sqrt[]{x+3}-2\right)\left(\sqrt[]{x+3}+2\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(\sqrt[]{x+3}+2\right)}{\left(x-1\right)\left(\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\sqrt[]{x+3}+2}{\sqrt[3]{\left(x-2\right)^2}-\sqrt[3]{x-2}+1}\)
\(=\dfrac{\sqrt[]{1+3}+2}{\sqrt[3]{\left(1-2\right)^2}-\sqrt[3]{1-2}+1}=\dfrac{4}{3}\)

3:
a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SBC) vuông góc (SAB)

\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1

8a.
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^+}\left(3x^2-5x+1\right)=3-5+1=-1\)
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\left(-3x+2\right)=-3+2=-1\)
\(\Rightarrow\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Rightarrow\) hàm có giới hạn tại \(x=1\)
Đồng thời \(\lim\limits_{x\rightarrow1}f\left(x\right)=-1\)
b.
\(\lim\limits_{x\rightarrow2^+}f\left(x\right)=\lim\limits_{x\rightarrow2^+}\dfrac{x^3-8}{x-2}=\lim\limits_{x\rightarrow2^+}\dfrac{\left(x-2\right)\left(x^2+2x+4\right)}{x-2}\)
\(=\lim\limits_{x\rightarrow2^+}\left(x^2+2x+4\right)=12\)
\(\lim\limits_{x\rightarrow2^-}f\left(x\right)=\lim\limits_{x\rightarrow2^-}\left(2x+1\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2^+}f\left(x\right)\ne\lim\limits_{x\rightarrow2^-}f\left(x\right)\Rightarrow\) hàm ko có giới hạn tại x=2
9.
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{x^2+mx+2m+1}{x+1}=\dfrac{0+0+2m+1}{0+1}=2m+1\)
\(\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2x+3m-1}{\sqrt{1-x}+2}=\dfrac{0+3m-1}{1+2}=\dfrac{3m-1}{3}\)
Hàm có giới hạn khi \(x\rightarrow0\) khi:
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\Rightarrow2m+1=\dfrac{3m-1}{3}\)
\(\Rightarrow m=-\dfrac{4}{3}\)



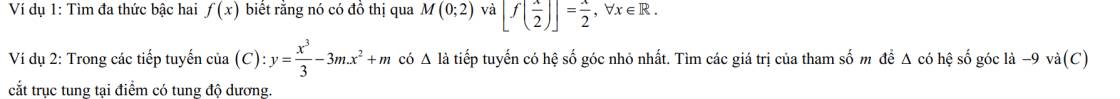 MỌI NGƯỜI GIÚP MÌNH HAI CÂU NÀY VỚI Ạ
MỌI NGƯỜI GIÚP MÌNH HAI CÂU NÀY VỚI Ạ 




6D