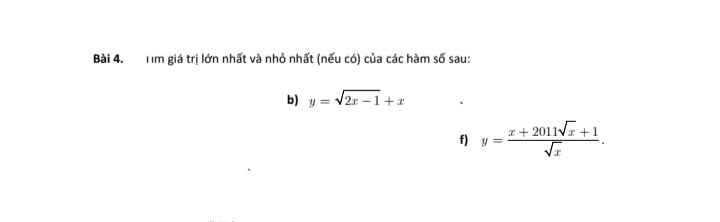L
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
3
29 tháng 9 2016
Do 1 số tự nhiên a chia cho 4 có các số dư là 0;1;2;3 ⇒ a sẽ có các dạng 4m; 4m +1
4m + 2 và 4m + 3 (m ∈ N). Với a = 4m ⇒ a² = 16m² = 4.4m² - có dạng 4k.
Với a = 4m + 1 ⇒ a² = (4m + 1)² = 16m² + 8m + 1 = 4(4m² + 2m) + 1 - có dạng 4k + 1
Với a = 4m + 2 ⇒ a² = (4m + 2)² = 16m² + 8m + 4 = 4(4m² + 2m + 1) - có dạng 4k
Với a = 4m + 3, lam tương tự ... a² = 4(4m² + 2m + 2) + 1 - có dạng 4k + 1
K
13 tháng 12 2020
11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
K
13 tháng 12 2020
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)
HH
1
25 tháng 1 2022
a: \(\overrightarrow{AB}=\left(-3;-2\right)\)
\(\overrightarrow{AC}=\left(1;-4\right)\)
Vì \(\overrightarrow{AB}< >\overrightarrow{AC}\) nên A,B,C ko thẳng hàng
hay A,B,C lập thành 1 tam giác
b: Gọi M là trung điểm của BC
\(\Leftrightarrow\left\{{}\begin{matrix}x_M=\dfrac{2-\left(-2\right)}{2}=2\\y_M=\dfrac{-1-1}{2}=-1\end{matrix}\right.\)
Vậy: M(2;-1)
A(1;3)
\(AM=\sqrt{\left(2-1\right)^2+\left(-1-3\right)^2}=\sqrt{17}\)
6 tháng 9 2021
Đặt y = f(x) = - 2x2 có đồ thị (C)
và y = g(x) = - 2x2 - 6x + 3 có đồ thị (C')
Ta có :
g(x) = - 2x2 - 6x + 3
= - 2\(\left(x^2+3x-\dfrac{3}{2}\right)\)
= - 2\(\left(x+\dfrac{3}{2}\right)^2\) + \(\dfrac{15}{2}\)
= \(f\left(x+\dfrac{3}{2}\right)+\dfrac{15}{2}\)
Vậy tịnh tiến (C) sang trái \(\dfrac{3}{2}\) đơn vị rồi kéo (C) lên trên \(\dfrac{15}{4}\) đơn vị ta được (C')
KB
12 tháng 4 2022
Có : 0 < \(\alpha< \dfrac{\pi}{2}\Rightarrow cos\alpha>0\) \(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{4}\right)^2}=\dfrac{\sqrt{7}}{4}\)
\(\Rightarrow sin2\alpha=2sin\alpha.cos\alpha=2.\dfrac{3}{4}.\dfrac{\sqrt{7}}{4}=\dfrac{3\sqrt{7}}{8}\)
\(cos2\alpha=1-2sin^2\alpha=1-2.\left(\dfrac{3}{4}\right)^2=-\dfrac{1}{8}\)
Ta có : \(A=\dfrac{cot2\alpha}{tan2\alpha+sin2\alpha}=\dfrac{1}{sin2\alpha+\dfrac{sin^22\alpha}{cos2\alpha}}=\dfrac{1}{\dfrac{3\sqrt{7}}{8}+\dfrac{\dfrac{63}{64}}{-\dfrac{1}{8}}}=\dfrac{8}{-63+3\sqrt{7}}\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 8 2021
b.
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\left\{{}\begin{matrix}\sqrt{2x-1}\ge0\\x\ge\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\sqrt{2x-1}+x\ge0+\dfrac{1}{2}=\dfrac{1}{2}\)
\(y_{min}=\dfrac{1}{2}\) khi \(x=\dfrac{1}{2}\)
b.
ĐKXĐ: \(x>0\)
\(y=\dfrac{x}{\sqrt{x}}+\dfrac{2011\sqrt{x}}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}=\sqrt{x}+\dfrac{1}{\sqrt{x}}+2011\ge2\sqrt{\dfrac{\sqrt{x}}{\sqrt{x}}}+2011=2013\)
\(y_{min}=2013\) khi \(\sqrt{x}=\dfrac{1}{\sqrt{x}}\Leftrightarrow x=1\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
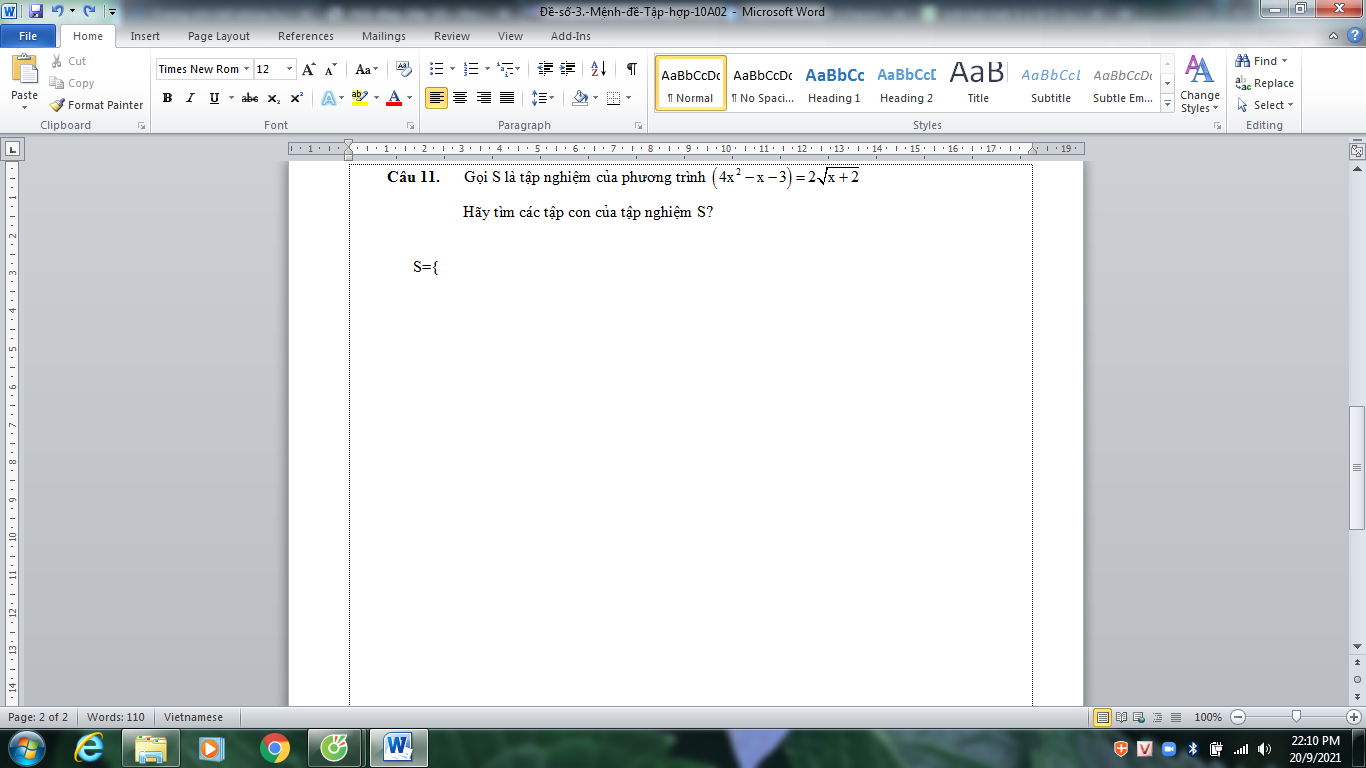
\(\Leftrightarrow4x^2=x+2+2\sqrt{x+2}+1\)
\(\Leftrightarrow\left(\sqrt{x+2}+1\right)^2=\left(2x\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x+2}+1=2x\\\sqrt{x+2}+1=-2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x+2}=2x-1\left(x\ge\dfrac{1}{2}\right)\\\sqrt{x+2}=-2x-1\left(x\le-\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+2=4x^2-4x+1\left(x\ge\dfrac{1}{2}\right)\\x+2=4x^2+4x+1\left(x\le-\dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{41}}{8}\\x=-1\end{matrix}\right.\)
