TN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HK
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2021
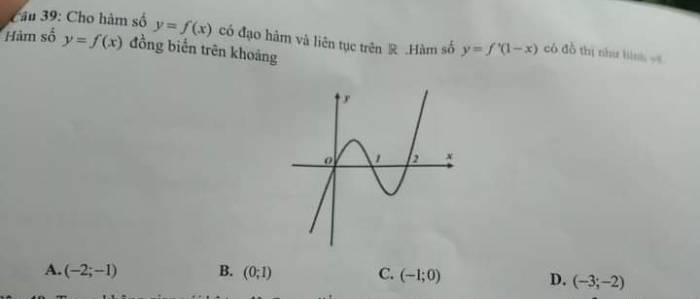
Đặt \(x=1-t\Rightarrow y=f\left(1-t\right)\Rightarrow y'=-f'\left(1-t\right)\) trái dấu với \(f'\left(1-t\right)\)
Từ đồ thị ta thấy \(f'\left(1-t\right)\) âm khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\) hay \(y'\) dương khi \(\left[{}\begin{matrix}t< 0\\1< t< 2\end{matrix}\right.\)
Hay \(\left[{}\begin{matrix}1-x< 0\\1< 1-x< 2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>1\\-1< x< 0\end{matrix}\right.\)
NM
Em có bài này muốn hỏi mọi người ạ, em đã cô lập được logy(x) nhưng tìm max min 2 ẩn vẫn khó quá :(.
2
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
Đề bài liệu có chính xác không nhỉ? Mình chỉ có thể tìm được max bằng \(2\sqrt{2}\) (xảy ra khi \(lnx=\sqrt{2}\) và \(lny=\dfrac{1}{2}\)) và ko thể tìm được min.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
À rồi OK, suy nghĩ hơi cồng kềnh 1 xíu nên hướng tìm min bị sai:
Giả thiết tương đương: \(y^{\sqrt{4-ln^2x}}=x^{1-lny}\)
\(\Rightarrow\sqrt{4-ln^2x}.lny=\left(1-lny\right)lnx\) (1)
Do \(y\ne1\Rightarrow lny\ne0\)
Nên (1) tương đương: \(\sqrt{4-ln^2x}=\left(\dfrac{1-lny}{lny}\right)lnx\) (2)
Đặt \(\left\{{}\begin{matrix}lnx=a\\lny=b\end{matrix}\right.\) thì \(log_yx=\dfrac{a}{b}\)
(2) trở thành: \(\sqrt{4-a^2}=\left(\dfrac{1-b}{b}\right)a\)
\(\Rightarrow\sqrt{4-a^2}=\dfrac{a}{b}-a\Rightarrow\dfrac{a}{b}=\sqrt{4-a^2}+a\)
Xét hàm \(f\left(a\right)=\sqrt{4-a^2}+a\) trên \(\left[-2;2\right]\)
\(f'\left(a\right)=1-\dfrac{a}{\sqrt{4-a^2}}=0\Rightarrow a=\sqrt{2}\)
\(f\left(-2\right)=-2\) ; \(f\left(\sqrt{2}\right)=2\sqrt{2}\) ; \(f\left(2\right)=2\)
\(\Rightarrow f\left(a\right)_{min}=-2\) ; \(f\left(a\right)_{max}=2\sqrt{2}\)
Đáp án B
3 tháng 10 2023
Đây là công thức bạn phải thuộc lòng, còn b là số lớn 0 và khác 1, tùy vào bài tập bạn giải sẽ có số b hợp lý.
mọi người chỉ em bài này với ạ. Em cảm ơn ạ!
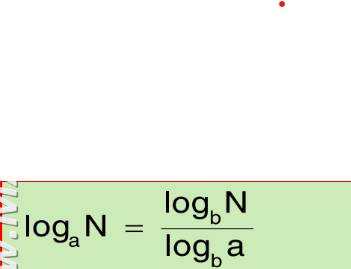
Một nghìn không trăm hai mươi chín phẩy bốn trăm tám mươi sáu tỷ đồng
một nghìn không trăm hai mươi chín phẩy bốn trăm tám mươi sáu tỷ đồng