mọi ng làm giúp minh với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 1 2023
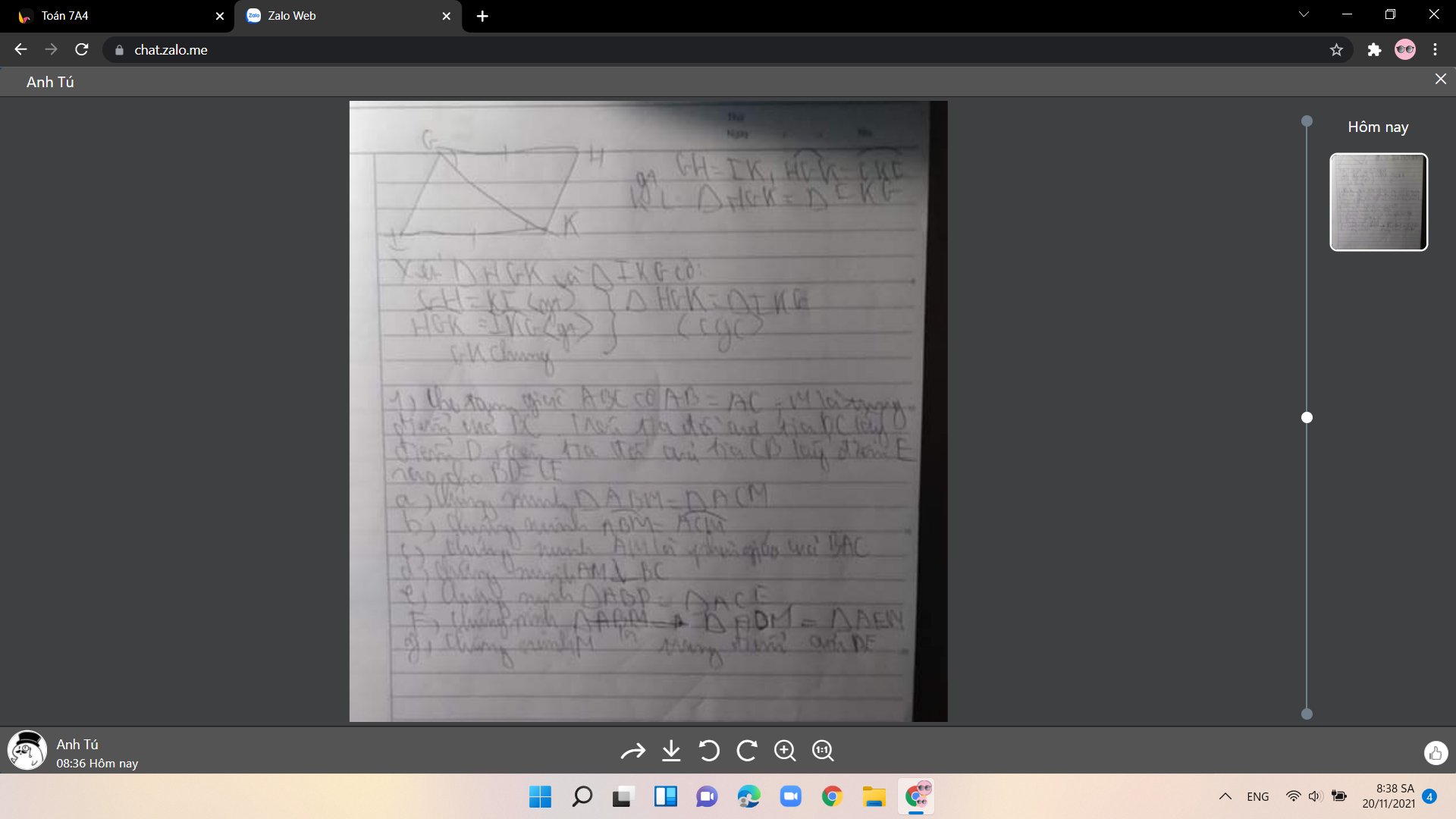
a: Xét ΔMAB và ΔMEC co
MA=ME
góc AMB=góc EMC
MB=MC
Do đó: ΔMAB=ΔMEC
b: ΔMAB=ΔMEC
=>góc MAB=góc MEC
=>AB//CE
c: AB//CE
AB vuông góc với CA
Do đo: CA vuông góc với CE
Xét tứ giác ABEC có
M làtrung điểm chung của AE và BC
góc BAC=90 độ
Do đó: ABEC là hình chữ nhật
=>ΔBEC vuông tại E
T
0
8 tháng 10 2021
Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{b}{a}=\dfrac{d}{c}\)
\(\Leftrightarrow1+\dfrac{b}{a}=1+\dfrac{d}{c}\)
\(\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
8 tháng 10 2021
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng t/c dtsbn:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\Leftrightarrow\dfrac{a+b}{a}=\dfrac{c+d}{c}\)
8 tháng 10 2021
\(\dfrac{a+5}{a-5}=\dfrac{b+6}{b-6}\Leftrightarrow\left(a+5\right)\left(b-6\right)=\left(a-5\right)\left(b+6\right)\\ \Leftrightarrow ab-6a+5b-30=ab+6a-5b-30\\ \Leftrightarrow12a=10b\\ \Leftrightarrow6a=5b\Leftrightarrow\dfrac{a}{b}=\dfrac{5}{6}\)
31 tháng 10 2021
a: \(P=-\left|5-x\right|+2019\le2019\forall x\)
Dấu '=' xảy ra khi x=5
31 tháng 10 2021
b) \(3^{n+2}-2^{n+2}+3^n-2^n=\left(3^n.3^2+3^n\right)-\left(2^{n-1}.2^3+2^{n-1}.2\right)\)
\(=3^n\left(3^2+1\right)-2^{n-1}\left(2^3+2\right)=3^n.10-2^{n-1}.10\)
\(=10\left(3^n-2^{n-1}\right)⋮10\)
8 tháng 10 2021
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}\\\dfrac{a}{c}=\dfrac{b}{d}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\left(\dfrac{a}{c}\right)^2=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\\\left(\dfrac{a}{c}\right)^2=\dfrac{ab}{cd}\end{matrix}\right.\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
16 tháng 8 2021
Bài 2:
a: Xét ΔACM và ΔNBM có
MA=MN
\(\widehat{AMC}=\widehat{NMB}\)
MC=MB
Do đó: ΔACM=ΔNBM
b: Xét ΔAMB và ΔNMC có
MA=MN
\(\widehat{AMB}=\widehat{NMC}\)
MB=MC
Do đó: ΔAMB=ΔNMC
Suy ra: AB=CN