
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD và ΔAMD có
AB=AM
\(\widehat{BAD}=\widehat{MAD}\)
AD chung
Do đó: ΔABD=ΔAMD
b: Ta có: ΔABD=ΔAMD
=>DB=DM
=>ΔDBM cân tại D
c: Ta có: AB=AM
=>A nằm trên đường trung trực của BM(1)
Ta có: DB=DM
=>D nằm trên đường trung trực của BM(2)
Từ (1) và (2) suy ra AD là đường trung trực của BM

16:
a: Xét ΔDHB vuông tại H và ΔEKC vuông tại K có
BD=CE
góc B=góc C
=>ΔDHB=ΔEKC
=>DH=EK
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AH=AK
HD=KE
=>ΔAHD=ΔAKE
=>AD=AE

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AD=AE
\(\widehat{HAD}=\widehat{KAE}\)
Do đó: ΔAHD=ΔAKE
Suy ra: HD=EK
c: Xét ΔABC có
AH/AB=AK/AC
nên HK//BC


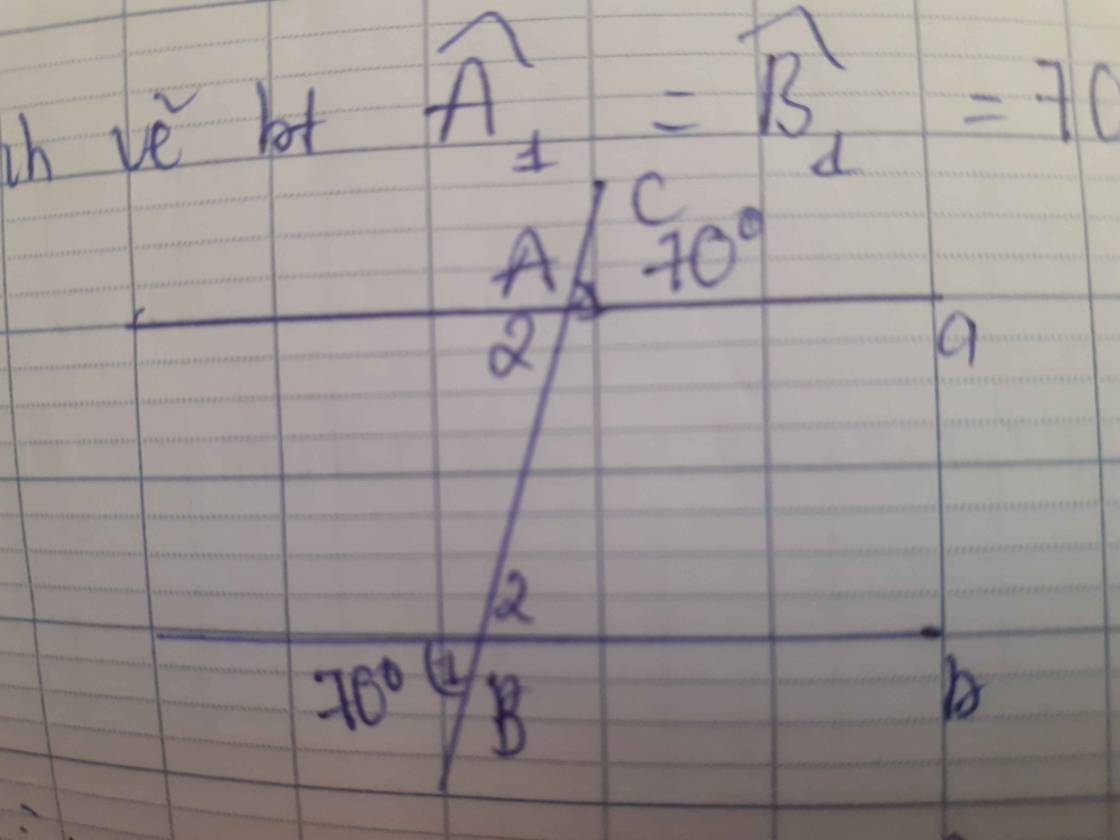
Ta có:
∠B₂ = ∠B₁ = 70⁰ (đối đỉnh)
⇒ ∠B₂ = ∠A₁ = 70⁰
Mà ∠B₂ và ∠A₁ là hai góc đồng vị
⇒ a // b

Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x-y}{2-3}=\dfrac{3}{-1}=-3\)
\(\Rightarrow\left\{{}\begin{matrix}x=-3.2=-6\\y=-3.3=-9\end{matrix}\right.\)

Áp dụng t/c dãy tỉ số bằng nhau:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{-18}{9}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=-2.2=-4\\y=-2.3=-6\\z=-2.4=-8\\\end{matrix}\right.\)

nếu muốn sửa đoạn đường trong 5 ngày thì số công nhân cần dùng đến là:
\(8\cdot10:5=16\left(người\right)\)



 Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều
Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều


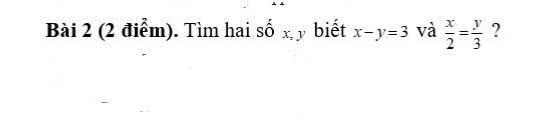
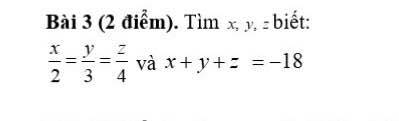

Xét ΔDEF có DE<DF<EF
mà \(\widehat{F};\widehat{E};\widehat{D}\) lần lượt là góc đối diện của các cạnh DE,DF,EF
nên \(\widehat{F}< \widehat{E}< \widehat{D}\)