K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 7 2021
a, \(=>R5nt\left[\left(R1ntR3\right)//\left(R2ntR4\right)\right]\)
\(=>Rtd=R5+\dfrac{\left(R1+R3\right)\left(R2+R4\right)}{R1+R2+R3+R\text{4}}\)
\(=2+\dfrac{\left(3+1\right)\left(2+2\right)}{3+1+2+2}=4\left(om\right)\)
b,\(=>Im=\dfrac{20}{4}=5A=I5\)\(=I1234\)
\(=>U1234=5.\dfrac{\left(3+1\right)\left(2+2\right)}{3+1+2+2}=10V=U24\)
\(=>I24=\dfrac{10}{2+2}=2,5A=IA\)
25 tháng 9 2021
:a) Điện trở tương đương toàn mạch:
\(R_{12}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{60.40}{60+40}=24\left(\Omega\right)\)
b) Vì \(R_1//R_2\Rightarrow U=U_1=U_2=I_{12}.R_{tđ}=0,5.24=12\left(V\right)\)
Cường độ dòng điện qua mỗi điện trở:
\(I_1=\dfrac{U_1}{R_1}=\dfrac{12}{60}=0,2\left(A\right)\\ I_2=\dfrac{U_2}{R_2}=\dfrac{12}{40}=0,3\left(\Omega\right)\)
c) \(\left(R_1//R_2\right)ntR_3\)
Công suất điện R1:
\(P_1=U_1.I_1=12.0,2=2,4\left(W\right)\)
Công suất điện R3:
\(P_3=\dfrac{P_1}{2}=\dfrac{2,4}{2}=1,2\left(W\right)\)
\(R_{12}ntR_3\Rightarrow I_{12}=I_3=0,5\left(A\right)\)
Hiệu điện thế 2 đầu R3:
\(P_3=U_3.I_3\rightarrow U_3=\dfrac{P_3}{I_3}=\dfrac{1,2}{0,5}=2,4\left(V\right)\)
Điện trở R3:
\(R_3=\dfrac{U_3}{I_3}=\dfrac{2,4}{0,5}=4,8\left(\Omega\right)\)
Ko chắc :v
28 tháng 9 2021
\(a,\)\(\Rightarrow\left\{{}\begin{matrix}Ud=Ub=3V\\Id=Idm=\dfrac{Ud}{Rd}=0,5A\end{matrix}\right.\)
\(\Rightarrow U1=U-Ud=6-3=3V\Rightarrow I1=\dfrac{U1}{R1}=0,75A\)
\(\Rightarrow Ib=I1-Id=0,25A\Rightarrow Rb=\dfrac{Ub}{Ib}=\dfrac{3}{0,25}=12\Omega\)
\(b,\Rightarrow Id=\dfrac{Ud}{Rd}=\dfrac{U-U1}{6}=\dfrac{6-Im.R1}{6}=\dfrac{6-\dfrac{6.4}{R1+\dfrac{Rb.Rd}{Rb+Rd}}}{6}=\dfrac{6-\dfrac{24}{\dfrac{24+10Rb}{6+Rb}}}{6}=\dfrac{36Rb}{6\left(24+10Rb\right)}=\dfrac{6Rb}{24+10Rb}=\dfrac{6}{\dfrac{24}{Rb}+10}\left(A\right)\)
\(\Rightarrow Rb\uparrow\Rightarrow\dfrac{24}{Rb}+10\downarrow\Rightarrow Id=\dfrac{6}{\dfrac{24}{Rb}+10}\uparrow\)
=>do sang den tang
Mn giúp mình với ạ
đây ạ mong chj giúp em
MN
27 tháng 6 2021
Sơ đồ mạch: R1 nt {[R2 nt (R3 // R4)] // (Ra nt Rx)}
\(R_{34}=\dfrac{R_3\cdot R_4}{R_3+R_4}=\dfrac{12\cdot12}{12+12}=6\left(\text{Ω}\right)\)
\(R_{234}=R_2+R_{34}=4+6=10\left(\text{Ω}\right)\)
\(R_{ax}=R_a+R_x=1+4=5\left(\text{Ω}\right)\)
\(R_{234ax}=\dfrac{R_{234}\cdot R_{ax}}{R_{234}+R_{ax}}=\dfrac{10\cdot5}{10+5}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{tđ}=R_1+R_{234ax}=10+\dfrac{10}{3}=\dfrac{40}{3}\left(\text{Ω}\right)\)
N
18 tháng 10 2021
Phần tự luận bạn tách ra giùm mình nhé, làm trắc nghiệm thoi =))
1. B
2. A
3. C
1. Bạn xem lại giúp mình nhé, tại tính R mà đơn vị lại là V???
2. D
MN
27 tháng 6 2021
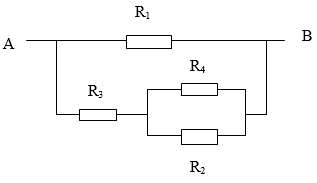
Sơ đồ mạch: R1 // [R3 nt (R2 // R4)]
\(R_{24}=\dfrac{R_2\cdot R_4}{R_2+R_4}=\dfrac{5\cdot10}{5+10}=\dfrac{10}{3}\left(\text{Ω}\right)\)
\(R_{234}=R_3+R_{24}=5+\dfrac{10}{3}=\dfrac{25}{3}\left(\text{Ω}\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{10\cdot\dfrac{25}{3}}{10+\dfrac{25}{3}}=\dfrac{50}{11}\left(\text{Ω}\right)\)
MN
27 tháng 6 2021
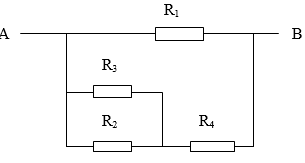
Sơ đồ mạch: R1 // [(R2 // R3) nt R4]
Điện trở tương đương là :
\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{4\cdot4}{4+4}=2\left(\text{Ω }\right)\)
\(R_{234}=R_{23}+R_4=6\left(\text{Ω }\right)\)
\(R_{AB}=\dfrac{R_1\cdot R_{234}}{R_1+R_{234}}=\dfrac{3\cdot6}{3+6}=2\left(\text{Ω }\right)\)
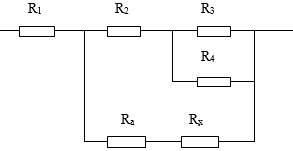
do \(\dfrac{R1}{R2}=\dfrac{R3}{R4}\)=>mạch cân bằng=>Ia=0A
\(=>\)