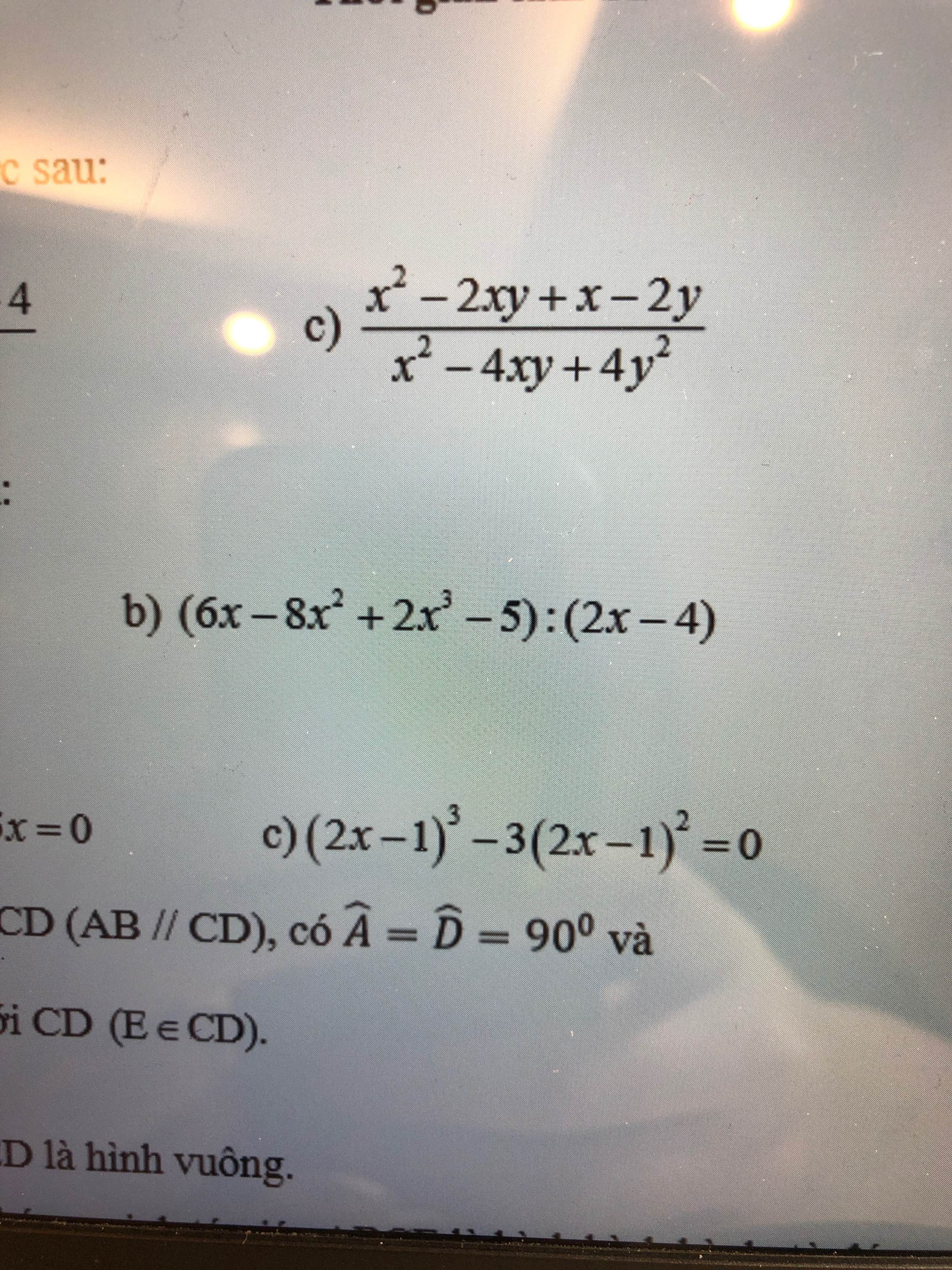K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Giúp mình với mn ơi:(
10 tháng 10 2021
a: Xét ΔADH vuông tại H và ΔBCI vuông tại I có
AD=BC
\(\widehat{D}=\widehat{C}\)
Do đó: ΔADH=ΔBCI
Suy ra: DH=CI
23 tháng 8 2021
a: Ta có: \(\dfrac{1-3x}{2x}-\dfrac{2-3x}{2x-1}-\dfrac{3x-2}{4x^2-2x}\)
\(=\dfrac{\left(1-3x\right)\left(2x-1\right)-2x\left(2-3x\right)-3x+2}{2x\left(2x-1\right)}\)
\(=\dfrac{2x-1+6x^2+3x-4x+6x^2-3x+2}{2x\left(2x-1\right)}\)
\(=\dfrac{12x^2-2x+1}{4x^2-2x}\)
b: Ta có: \(\dfrac{x+2}{x^3-1}-\dfrac{-2}{x^2+x+1}-\dfrac{1}{x+1}\)
\(=\dfrac{x+2+2x-2}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{x^3-1}{\left(x+1\right)\left(x-1\right)\left(x^2+x+1\right)}\)
\(=\dfrac{3x^2+3x-x^3+1}{\left(x+1\right)\left(x-1\right)\left(x^2+x+1\right)}\)
H9
HT.Phong (9A5)
CTVHS
29 tháng 7 2023
Bài 1: Ta có:
\(A=\dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}\)
\(A=\dfrac{a^3}{abc}+\dfrac{b^3}{abc}+\dfrac{c^3}{abc}\)
\(A=\dfrac{a^3+b^3+c^3}{abc}\) (2)
Mà: \(a+b+c=0\)
\(\Rightarrow\left(a+b+c\right)^3=0\)
\(\Rightarrow a^3+b^3+c^3+3a^2b+3ab^2+3b^2c+3bc^2+3a^2c+3ac^2+6abc=0\)
\(\Rightarrow a^3+b^3+c^3+\left(3a^2b+3ab^2+3abc\right)+\left(3b^2c+3bc^2+3abc\right)+\left(3a^2c+3ac^2+3abc\right)-3abc=0\)
\(\Rightarrow a^3+b^3+c^3+3ab\left(a+b+c\right)+3ac\left(a+b+c\right)+3bc\left(a+b+c\right)-3abc=0\)
\(\Rightarrow a^3+b^3+c^3+\left(a+b+c\right)\left(3ab+3ac+3bc\right)-3abc=0\) (1)
Thay \(a+b+c=0\) (1) ta có:
\(a^3+b^3+c^3+0\cdot\left(3ab+3ac+3bc\right)-3abc=0\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\Rightarrow a^3+b^3+c^3=3abc\)
Thay vào (2) ta có:
\(\dfrac{3abc}{abc}=3\)
ậy
29 tháng 7 2023
1:
a+b=c=0
=>a+b=-c; a+c=-b; b+c=-a
\(A=\dfrac{a^3+b^3+c^3}{abc}\)
\(=\dfrac{\left(a+b\right)^3-3ab\left(a+b\right)+c^3}{abc}=\dfrac{\left(-c\right)^3+3bac+c^3}{abc}\)
=3abc/abc=3
NG
1
28 tháng 11 2021
\(\dfrac{x-1}{x^2+5x}=\dfrac{\left(x-1\right)\left(x-5\right)}{x\left(x-5\right)\left(x+5\right)};\dfrac{x+1}{x^2-25}=\dfrac{x\left(x+1\right)}{x\left(x-5\right)\left(x+5\right)}\)
19 tháng 10 2021
Bài 3:
c: \(5x\left(x-1\right)+3y\left(x-1\right)=\left(x-1\right)\left(5x+3y\right)\)
d: \(x\left(x+y\right)-12x-12y=\left(x+y\right)\left(x-12\right)\)
NN
1
24 tháng 11 2021
\(2b,=\left(2x^3-4x^2-4x^2+8x-2x+4-9\right):\left(2x-4\right)\\ =\left[\left(2x-4\right)\left(x^2-2x-2\right)-9\right]:\left(2x-4\right)\\ =x^2-2x-2\left(\text{ dư -9}\right)\)