
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{3\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}+2}{\sqrt{a}+1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{3a+3\sqrt{a}-\left(a-\sqrt{a}+2\sqrt{a}-2\right)}{\sqrt{a}}\)
\(=2+\dfrac{3a+3\sqrt{a}-a+\sqrt{a}-2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}+2a+2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\left(a+2\sqrt{a}+1\right)}{\sqrt{a}}\)
\(=\dfrac{2\left(\sqrt{a}+1\right)^2}{\sqrt{a}}\)
b) Ta có: \(P-6=\dfrac{2\left(\sqrt{a}+1\right)^2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2a+4\sqrt{a}+2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\left(a-\sqrt{a}+1\right)}{\sqrt{a}}>0\forall a\) thỏa mãn ĐKXĐ
hay P>6

a) Ta có: \(A=\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
b) Thay \(x=7+4\sqrt{3}\) vào A, ta được:
\(A=\dfrac{2+\sqrt{3}+2}{2+\sqrt{3}-2}=\dfrac{4+\sqrt{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}+3}{3}\)
c) Ta có: \(M=\dfrac{x+5}{\sqrt{x}-2}:\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x+5}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow M\ge2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4\)
\(\Leftrightarrow M\ge2\cdot3-4=6-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=3\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1

1) \(\sqrt{2x-5}=7\)
\(\left(\sqrt{2x-5}\right)^2=7^2\)
\(2x-5=49\)
\(2x=54\)
\(x=27\)
2) \(3+\sqrt{x-2}=4\)
\(\sqrt{x-2}=1\)
\(\left(\sqrt{x-2}\right)^2=1^2\)
\(x-2=1\)
\(x=3\)
1) \(\sqrt{2x-5}=7\left(đk:x\ge\dfrac{5}{2}\right)\)
\(\Leftrightarrow2x-5=49\Leftrightarrow2x=54\Leftrightarrow x=27\left(tm\right)\)
2) \(3+\sqrt{x-2}=4\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{x-2}=1\Leftrightarrow x-2=1\Leftrightarrow x=3\)
3) \(\Leftrightarrow\sqrt{\left(x-1\right)^2}=1\Leftrightarrow\left|x-1\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\)
4) \(\Leftrightarrow\sqrt{\left(x-2\right)^2}=1\Leftrightarrow\left|x-2\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=1\\x-2=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
5) \(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=\sqrt{\left(x+4\right)^2}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x+4\\2x-1=-x-4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
6) \(ĐK:x\ge-2\)
\(\Leftrightarrow5\sqrt{x+2}-3\sqrt{x+2}-\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow\sqrt{x+2}=\sqrt{x+7}\)
\(\Leftrightarrow x+2=x+7\Leftrightarrow2=7\left(VLý\right)\)
Vậy \(S=\varnothing\)
7) \(ĐK:x\ge-1\)
\(\Leftrightarrow5\sqrt{2x+1}+3\sqrt{x+1}=4\sqrt{x+1}+4\sqrt{2x+1}\)
\(\Leftrightarrow\sqrt{2x+1}=\sqrt{x+1}\)
\(\Leftrightarrow2x+1=x+1\Leftrightarrow x=0\left(tm\right)\)

\(a,\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\\ =\sqrt{\sqrt{5}-\sqrt{3-\left(2\sqrt{5}-3\right)}}\\ =\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}\\ =\sqrt{\sqrt{5}-\left(\sqrt{5}-1\right)}\\ =\sqrt{1}=1\)
\(b,\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\\ =\sqrt{13+30\sqrt{2+\left(2\sqrt{2}+1\right)}}\\ =\sqrt{13+30\sqrt{3+2\sqrt{2}}}\\ =\sqrt{13+30\left(\sqrt{2}+1\right)}\\ =\sqrt{43+30\sqrt{2}}\\ =5+3\sqrt{2}\)
\(c,\sqrt{1+\sqrt{3+\sqrt{13+4\sqrt{3}}}}+\sqrt{1-\sqrt{3-\sqrt{13-4\sqrt{3}}}}\\ =\sqrt{1+\sqrt{3+\left(2\sqrt{3}+1\right)}}+\sqrt{1-\sqrt{3-\left(2\sqrt{3}-1\right)}}\\ =\sqrt{1+\sqrt{4+2\sqrt{3}}}+\sqrt{1-\sqrt{4-2\sqrt{3}}}\\ =\sqrt{1+\left(\sqrt{3}+1\right)}+\sqrt{1-\left(\sqrt{3}-1\right)}\\ =\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
Đặt \(A=\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
\(A^2=4+2\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=4+2=6\\ A=\sqrt{6}\)
Vậy gt biểu thức là \(\sqrt{6}\)
\(d,\sqrt{5-\sqrt{13+4\sqrt{3}}}+\sqrt{3+\sqrt{13+4\sqrt{3}}}\\ =\sqrt{5-\left(2\sqrt{3}+1\right)}+\sqrt{3+\left(2\sqrt{3}+1\right)}\\ =\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}\\ =\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)
\(4,\)
\(A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\\ A^2=2-\sqrt{3}+2+\sqrt{3}+2\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\\ A^2=4+2=6\\ A=\sqrt{6}\\ B=\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\\ B^2=4-\sqrt{7}+4+\sqrt{7}-2\sqrt{\left(4-\sqrt{7}\right)\left(4+\sqrt{7}\right)}\\ B^2=8-2\sqrt{9}=8-6=2\\ B=\sqrt{2}\)
\(5,\\ a,\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\\ =\sqrt{\left(\sqrt{2}+\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\sqrt{2}+\sqrt{3}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\\ b,\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}\\ =\left(\sqrt{5}-\sqrt{2}\right)-\left(\sqrt{2}+\sqrt{5}\right)=-2\sqrt{2}\\ c,\sqrt{24+8\sqrt{5}}+\sqrt{9-4\sqrt{5}}\\ =\left(2\sqrt{5}-2\right)+\left(\sqrt{5}-2\right)\\ =3\sqrt{5}\\ d,\sqrt{17-12\sqrt{2}}+\sqrt{9+4\sqrt{2}}\\ =\left(3-2\sqrt{2}\right)+\left(2\sqrt{2}+1\right)\\ =4\)


ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm



\(\Leftrightarrow\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\2x^2+2x^2y^2-4y=0\left(1\right)\end{matrix}\right.\Rightarrow}x^3+2y^2-4y-2x^2-2x^2y^2+4y=0\Rightarrow x^3+1-2x^2y^2+2y^2-2x^2+2=0\Rightarrow\left(x+1\right)\left(x^2-x+1\right)-2y^2\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(x^2-x+1-2xy^2+2y^2-2x+2\right)=0\Rightarrow x=-1\)Thay x=-1 vào (1) ta được y2-2y+1=0⇒ (y-1)2=0⇒y-1=0⇒y=1
Do đó Q=x2+y2=(-1)2+12=2
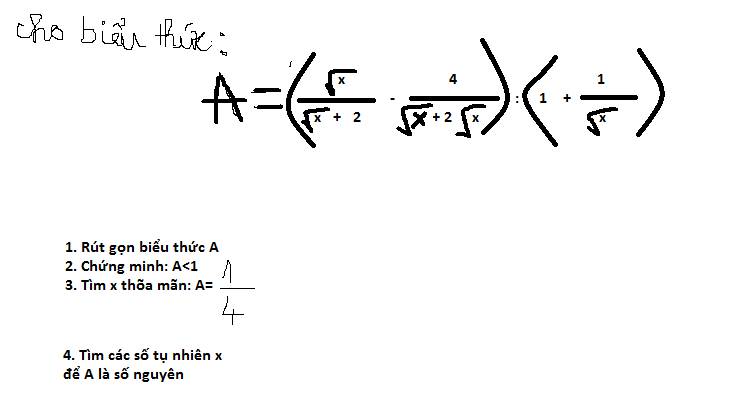

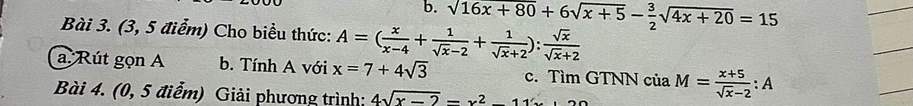 mn giúp em phần tìm gtnn vs ạ, em cần gấp
mn giúp em phần tìm gtnn vs ạ, em cần gấp




1: \(A=\dfrac{x-4}{\sqrt{x}\left(\sqrt{x}+2\right)}:\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}\)
2: căn x-2<căn x+1
=>A<1
3: A=1/4
=>căn x-2/căn x+1=1/4
=>4 căn x-8=căn x+1
=>3 căn x=9
=>x=9