
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right).\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{1}{\sqrt{x}+1}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow B=\dfrac{1}{\sqrt{x}}\)

Bài 1:
ĐKXĐ: $x>0; x\neq 1$
\(A=\frac{(\sqrt{x}-1)(x+\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}-1)}-\frac{(\sqrt{x}+1)(x-\sqrt{x}+1)}{\sqrt{x}(\sqrt{x}+1)}+\frac{x+1}{\sqrt{x}}\)
\(=\frac{x+\sqrt{x}+1}{\sqrt{x}}-\frac{x-\sqrt{x}+1}{\sqrt{x}}+\frac{x+1}{\sqrt{x}}=\frac{x+\sqrt{x}+1-(x-\sqrt{x}+1)+(x+1)}{\sqrt{x}}\)
\(=\frac{x+2\sqrt{x}+1}{\sqrt{x}}=\frac{(\sqrt{x}+1)^2}{\sqrt{x}}\)
Bài 2:
\(\frac{x+2}{x\sqrt{x}+1}+\frac{\sqrt{x}-1}{x-\sqrt{x}+1}-\frac{\sqrt{x}-1}{x-1}\)
\(=\frac{x+2}{(\sqrt{x}+1)(x-\sqrt{x}+1)}+\frac{(\sqrt{x}-1)(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{\sqrt{x}-1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)
\(=\frac{x+2+x-1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{1}{\sqrt{x}+1}=\frac{2x+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}-\frac{x-\sqrt{x}+1}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{2x+1-(x-\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{x+\sqrt{x}}{(\sqrt{x}+1)(x-\sqrt{x}+1)}\)
\(=\frac{\sqrt{x}(\sqrt{x}+1)}{(\sqrt{x}+1)(x-\sqrt{x}+1)}=\frac{\sqrt{x}}{x-\sqrt{x}+1}\)
Theo BĐT Cô-si:
$x+1\geq 2\sqrt{x}\Rightarrow x-\sqrt{x}+1\geq \sqrt{x}$
$\Rightarrow B\leq \frac{\sqrt{x}}{\sqrt{x}}=1$
Dấu "=" xảy ra khi $x=1$ (không thỏa mãn vì $x\neq 1$)
$\Leftrightarrow B< 1$

1
Có: \(tgB=\dfrac{CA}{CB}=\dfrac{0,9}{1,2}=\dfrac{3}{4}\)
\(cotgB=\dfrac{CB}{CA}=\dfrac{1,2}{0,9}=\dfrac{4}{3}\)
Vì A, B phụ nhau nên:
\(cotgA=tgB=\dfrac{3}{4}\\ tgA=cotgB=\dfrac{4}{3}\)
Áp dụng pytago vào tam giác ABC vuông tại C, có:
\(AB^2=BC^2+AC^2=1,2^2+0,9^2=1,5^2\Rightarrow AB=1,5\left(vì.AB>0\right)\)
Do đó: \(sinB=\dfrac{CA}{AB}=\dfrac{0,9}{1,5}=\dfrac{3}{5};cosB=\dfrac{CB}{BA}=\dfrac{1,2}{1,5}=\dfrac{4}{5}\)
Vì A, B phụ nhau nên:
\(sinA=cosB=\dfrac{4}{5};cosA=sinB=\dfrac{3}{5}\)
3:
a: Xét ΔBAC có AB^2=CA^2+CB^2
nên ΔABC vuông tại C
b: sin A=cos B=BC/AC=căn 15/5
cos A=sin A=CA/BC=căn 2/5=1/5*căn 10
tan A=cot B=căn 15/căn 10=căn 3/2
cot A=tan B=căn 2/3

Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)

\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)

`48/[x+4]+48/[x-4]=5` `ĐK: x \ne +-4`
`<=>[48(x-4)+48(x+4)]/[(x-4)(x+4)]=[5(x+4)(x-4)]/[(x-4)(x+4)]`
`=>48x-192+48x+192=5x^2-80`
`<=>5x^2-96x-80=0`
`<=>5x^2-100+4x-80=0`
`<=>5x(x-20)+4(x-20)=0`
`<=>(x-20)(5x+4)=0`
`<=>` $\left[\begin{matrix} x=20\\ x=\dfrac{-4}{5}\end{matrix}\right.$ (t/m)
Vậy `S={-4/5;20}`
ĐK : \(x\ne\pm4\)
\(\Leftrightarrow\cdot\dfrac{48\left(x+4\right)+48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow48x+192+48x-192==5x^2-80\)
\(\Leftrightarrow96x=5x^2-80\)
\(\Leftrightarrow5x^2-96x-80=0\)
\(\Leftrightarrow5x^2+4x-100-80=0\)
\(\Leftrightarrow4\left(x-20\right)+5x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\5x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-\dfrac{4}{5}\end{matrix}\right.\)

Bạn tự vẽ hình nhan với bạn có ghi lộn chỗ MP với tính góc P thành MB với góc B ko nhan nếu lộn thì bài làm như sau:
a/Xét tam giác MNP,góc N=90độ,có:
MP^2=NP^2+MN^2(pytago)
=>NP^2=MP^2-MN^2
NP^2=17^2-8^2
NP^2=225
NP= căn bậc của 225=15
b/ Ta có: sinM=NP/MP=15/17
=> góc M≈62độ
sinP=MN/MP=8/17
=> góc P≈28độ
Sửa đề: MP = 17
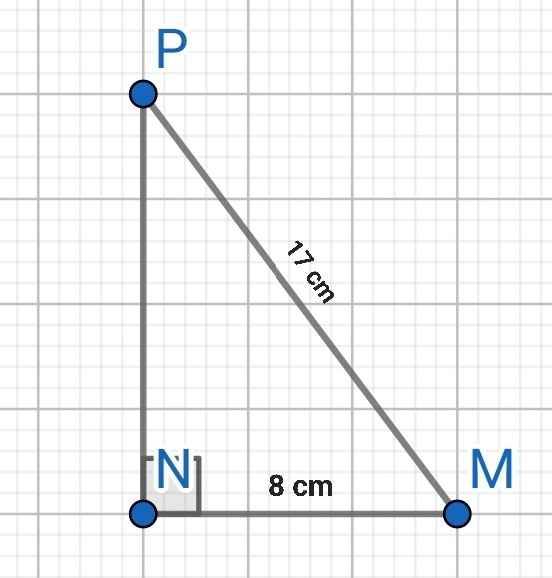 a) MNP vuông tại N
a) MNP vuông tại N
⇒ MP² = MN² + NP² (Pytago)
⇒ NP² = MP² - MN²
= 17² - 8²
= 225
⇒ NP = 15 (cm)
b) Sửa đề: Tính ∠M và ∠P
Ta có:
sin M = NP/MP = 15/17
⇒ ∠M ≈ 62⁰
⇒ ∠P ≈ 90⁰ - ∠M = 90⁰ - 62⁰ = 28⁰

\(\Leftrightarrow\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\2x^2+2x^2y^2-4y=0\left(1\right)\end{matrix}\right.\Rightarrow}x^3+2y^2-4y-2x^2-2x^2y^2+4y=0\Rightarrow x^3+1-2x^2y^2+2y^2-2x^2+2=0\Rightarrow\left(x+1\right)\left(x^2-x+1\right)-2y^2\left(x-1\right)\left(x+1\right)-2\left(x-1\right)\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(x^2-x+1-2xy^2+2y^2-2x+2\right)=0\Rightarrow x=-1\)Thay x=-1 vào (1) ta được y2-2y+1=0⇒ (y-1)2=0⇒y-1=0⇒y=1
Do đó Q=x2+y2=(-1)2+12=2
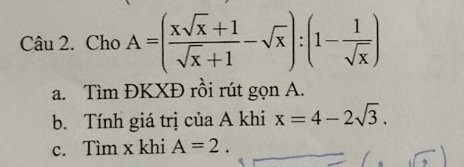
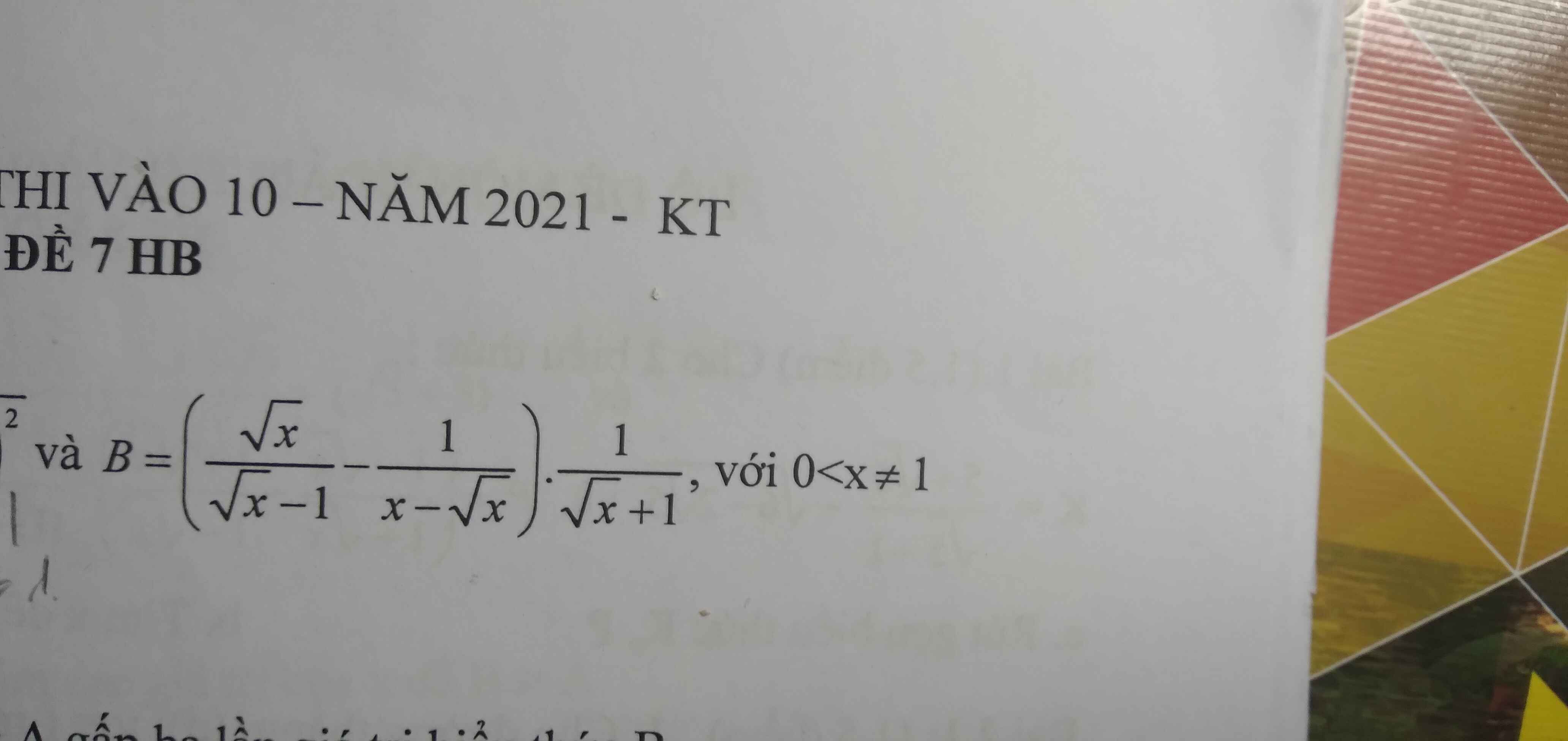
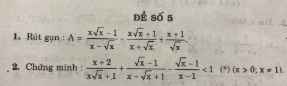 Mn giúp mình bài 2 vs ạ
Mn giúp mình bài 2 vs ạ



a: ĐKXĐ: x>0
\(A=\left(x-\sqrt{x}+1-\sqrt{x}\right):\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)\)=x-căn x
b: Khi x=4-2căn 3 thì A=4-2căn 3-(căn 3-1)
=4-2căn 3-căn 3+1
=5-3căn 3
c: A=2
=>x-căn x=2
=>x-căn x-2=0
=>(căn x-2)(căn x+1)=0
=>căn x-2=0
=>x=4