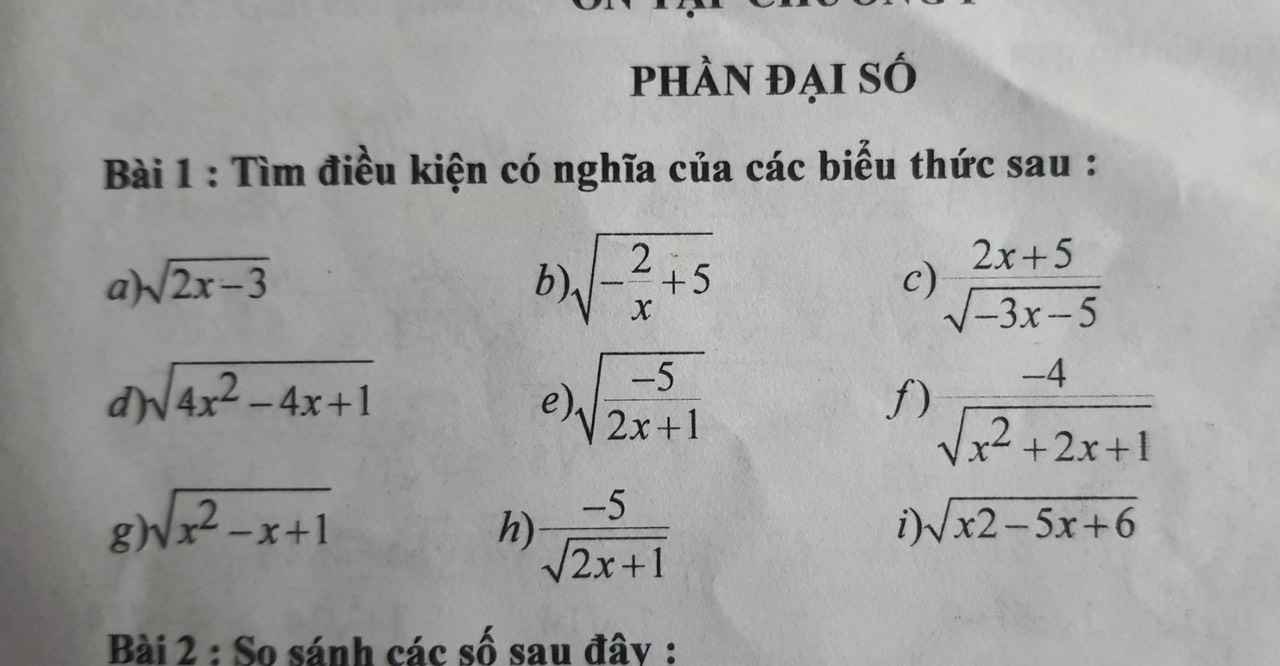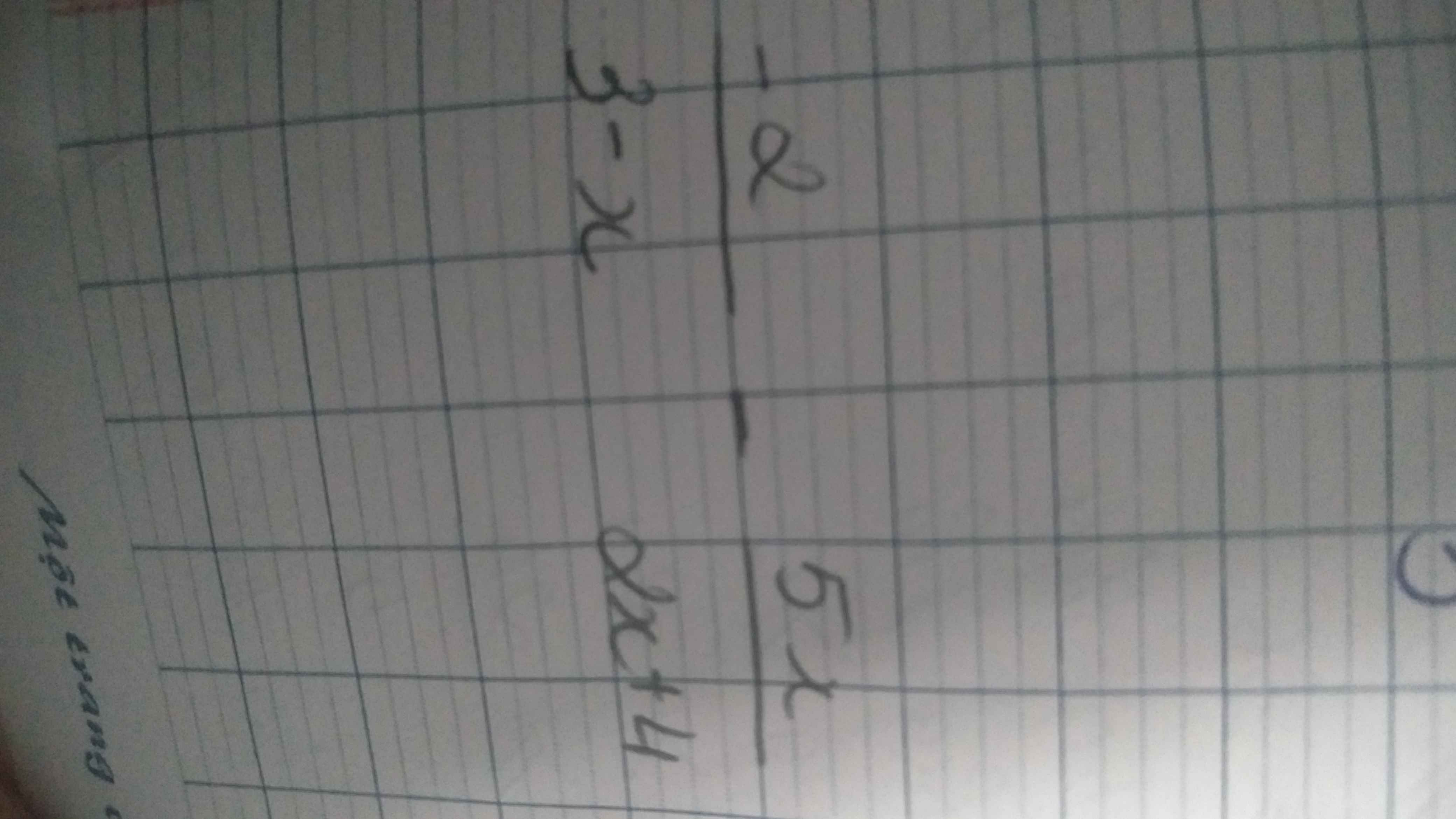Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) ĐKXĐ: \(2x-3\ge0\Rightarrow x\ge\dfrac{3}{2}\)
b) ĐKXĐ: \(-\dfrac{2}{x}+5\ge0\Rightarrow x\ge\dfrac{2}{5}\)
c)ĐKXĐ: \(-3x-5>0\Rightarrow x>-\dfrac{5}{3}\)
d) ĐKXĐ: \(4x^2-4x+1\ge0\Rightarrow\left(2x-1\right)^2\ge0\) (luôn đúng)

a: Xét tứ giác AOBM có
góc OAM+góc OBM=180 độ
=>AOBM nội tiếp
b: \(cosAOM=\dfrac{OA}{OM}=\dfrac{1}{3}\)
nên \(\widehat{AOM}\simeq71^0\)
=>\(\widehat{AOB}\simeq142^0\)
=>sđ cung nhỏ AB là 142 độ; sđ cung lơn AB=360-142=218 độ
c:
Xét (O) có
ΔBAC nội tiếp
BC là đường kính
=>ΔBAC vuông tại A
=>BA vuông góc AC
Xét(O) có
MA,MB là tiêp tuyến
nên MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM//AC
góc ACB=góc OAC
góc OAC=góc AOM
=>góc ACB=góc AOM=góc BOM
d: góc DOM+góc BOM=90 độ
góc DMO+góc AOM=90 độ
mà góc BOM=góc AOM
nên góc DOM=góc DMO
=>DO=DM

\(\dfrac{-2}{3-x}-\dfrac{5x}{2x+4}\)
ĐKXĐ: \(\left\{{}\begin{matrix}3-x\ne0\\2x+4\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-2\end{matrix}\right.\)

A=\(\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}+2\right)^2}{1-\sqrt{x}}\)=\(\dfrac{\sqrt{x}+2}{\sqrt{x}}\)

1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

a: Xét (O) có
OI là một phần đường kính
DE là dây
I là trung điểm của DE
DO đó; OI⊥DE
Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
nên A,B,O,C cùng thuộc đường tròn(1)
Xét tứ giác OIAC có \(\widehat{OIA}+\widehat{OCA}=180^0\)
nên OIAC là tứ giác nội tiếp(2)
Từ (1) và (2) suy ra A,I,O,B,C cùng thuộc đường tròn
b: Xét ΔABD và ΔAEB có
\(\widehat{ABD}=\widehat{AEB}\)
\(\widehat{BAD}\) chung
Do đó:ΔABD∼ΔAEB
Suy ra: AB/AE=AD/AB
hay \(AB^2=AD\cdot AE\)
Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(3)
Ta có: OB=OC
nên O nằm tren đường trung trực của BC(4)
Từ (3) và (4) suy ra OA⊥BC

 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !