
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Dự đoán khi a=b=1, ta chỉ cần xét thằng F = 9($\frac{1}{a^2}$ + $\frac{1}{b^2}$) - 6($\frac{a}{b}$ + $\frac{b}{a}$) lớn hơn hoặc bằng cái gì đó là xong . Thì ta có :
F = 9.$\frac{a^2 + b^2}{a^2b^2}$ - 6. $\frac{a^2+b^2}{ab}
= $\frac{a^2+b^2}{ab}$.($\frac{9}{ab}$ - 6)
Lại có $a^2 + b^2$ > 2ab (BĐT côsi )
=> $\frac{a^2+b^2}{ab}$ > 2
Và $\frac{9}{ab}$ - 6 > $\frac{9}{\frac{(a+b)^2}{4}}$ - 6 = 3
=> F > 6
Mà 2($a^2 + b^2$) > $(a+b)^2$ = 4
=> Q > 4+ F > 10
Dấu " = " <=> a=b=1. ^^

a: Δ=(2m+2)^2-4(4m-m^2)
=4m^2+8m+4-16m+4m^2
=8m^2-8m+4
=8m^2-8m+2+2
=2(2m-1)^2+2>=2>0 với mọi m
=>Phương trình luôn có hai nghiệm phân biệt
b: \(E=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=\sqrt{\left(2m+2\right)^2-4\left(4m-m^2\right)}\)
\(=\sqrt{4m^2+8m+4-16m+4m^2}\)
\(=\sqrt{8m^2-8m+4}\)
\(=\sqrt{8m^2-8m+2+2}=\sqrt{2\left(2m-1\right)^2+2}>=\sqrt{2}\)
Dấu = xảy ra khi m=1/2


\(a,A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(2\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\\ b,A=\dfrac{2\left(\sqrt{x}+1\right)-3}{\sqrt{x}+1}=2-\dfrac{3}{\sqrt{x}+1}\in Z\\ \Leftrightarrow\sqrt{x}+1\inƯ\left(3\right)=\left\{1;3\right\}\left(\sqrt{x}+1\ge1\right)\\ \Leftrightarrow\sqrt{x}\in\left\{0;2\right\}\\ \Leftrightarrow x\in\left\{0;4\right\}\left(tm\right)\)
a) \(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(\Rightarrow A=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2x-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2x-2\sqrt{x}\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Rightarrow A=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)

Gọi chiều rộng là x
Chiều dài là 17-x
Theo đề, ta có: \(\left(x+2\right)\left(20-x\right)=x\left(17-x\right)+45\)
\(\Leftrightarrow20x-x^2+40-2x=17x-x^2+45\)
=>18x+40=17x+45
=>x=5
Vậy: Chiều rộng là 5m
Chiều dài là 12m


a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật
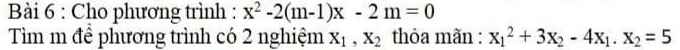


 Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Mn giúp mình bài 3 với ạ. Mình đang cần gấp lắm. Mình cảm ơn nhiều !
Hình thì bạn tự vẽ nhé.
Bài 1:
Với 3 điểm O, A, B cùng thuộc một mặt phẳng, ta luôn có: \(AB\le OA+OB\)
Mà OA = OB = R \(\Rightarrow AB\le R+R=2R\)
Vì 2R chính là đường kính của đường tròn nên ta rút ra được nhận xét: Trong một đường tròn, đường kính là dây lớn nhất.
Bài 2:
Bạn xem lại đề bài này, hình như phải là "Chứng minh I là trung điểm của CD" chứ.
Dễ thấy OC = OD (= bán kính của (O)) \(\Rightarrow\Delta OCD\)cân tại O
Lại có \(OI\perp CD\)tại I (điều này là hiển nhiên vì \(AB\perp CD\)tại I và O thuộc AB)
\(\Rightarrow\)OI là trung tuyến của \(\Delta OCD\)(tính chất tam giác cân) \(\Rightarrow\)I là trung điểm CD